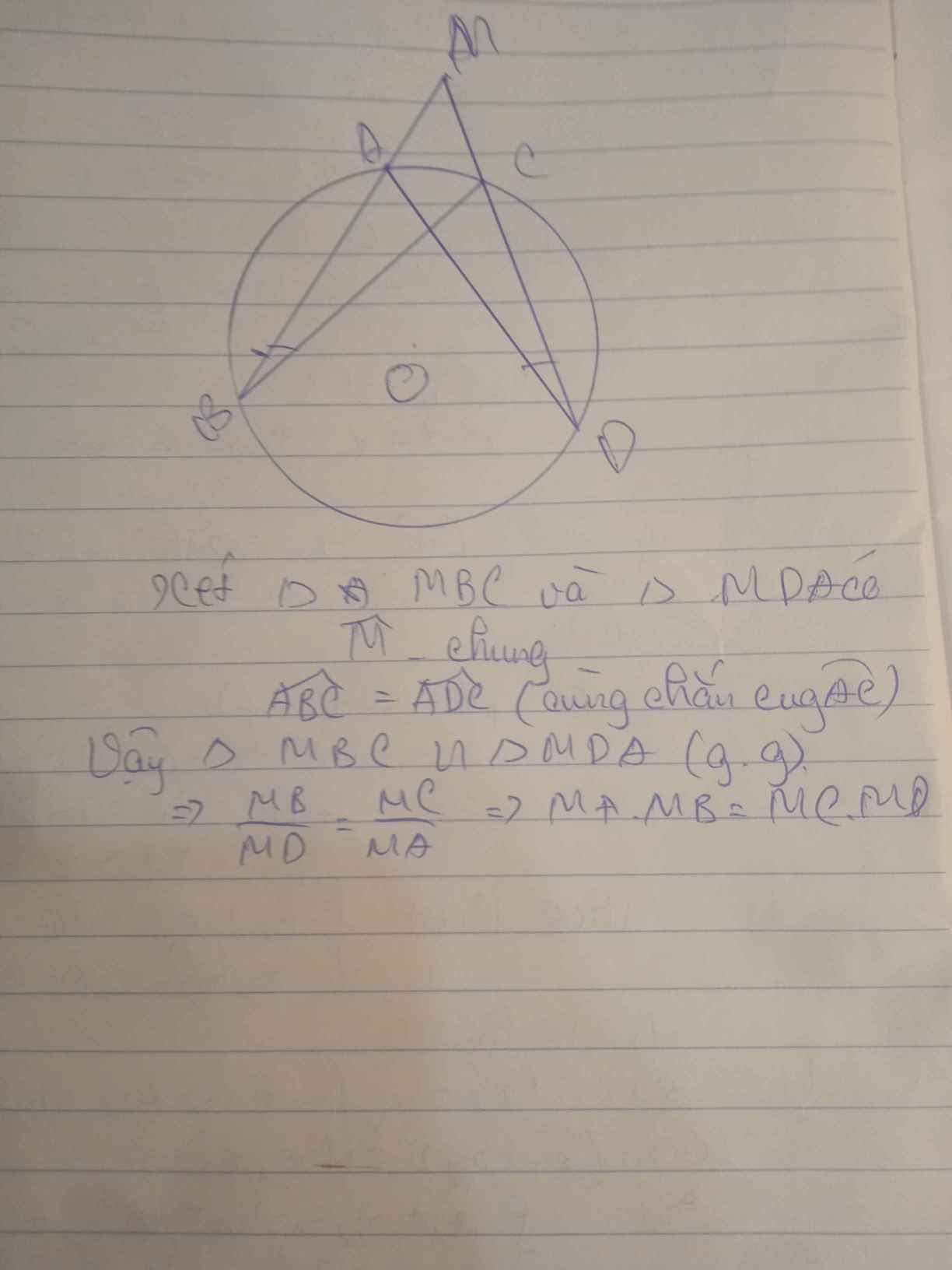từ M nằm ngoài (O) kẻ tiếp tuyến MA, MB và cát tuyến MCD (MC<MD). Gọi E là trung điểm CD, MO cắt (O) và AB ở I và H. AE cắt (O) ở S. Chứng minh BS song song CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
9 tháng 2 2022
Xét (O) có:
CDA và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc CDA = góc ABC hay góc MDA= gócMBC
Xét tam giác MDA và tam giác MBC có:
góc MDA = góc MBC(cmt)
góc M chung
=> 2 tam giác trên đồng dạng(g.g)
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD
10 tháng 5 2023
MC*MD=MH*MO
=>ΔMHC đồng dạng với ΔMDO
=>OHCD nội tiếp
=>góc OHD=góc OCD
=>góc OHD=góc MHC
GỌi K là giao của AB và CD
=>90 độ-góc OHD=90 độ-góc MHC
=>góc DHK=góc KHC
=>HK là phân giác của góc PHC
Vì NM vuông góc HK
nên HM là phân giác góc ngoài của góc PHC
=>MC/MD=HC/HD; CK/DK=HC/HD
=>MC/MD=CK/DK
CP//AD
=>CP/AD=MC/MD
CQ//AD
=>CQ/AD=CK/DK
=>CP/AD=CQ/AD
=>CP=CQ
=>ĐPCM
11 tháng 5 2023
MC*MD=MH*MO
=>MC/MO=MH/MD
=>ΔMCH đồng dạng với ΔMOD
=>goc MHC=góc MDO=góc ODC
=>OHCD nội tiếp
=>góc OHD=góc OCD
ΔOCD cân tại O nên góc ODC=góc OCD
=>góc OHD=góc MHC
=>90 dộ-góc OHD=90 độ-góc MHC(1)
Gọi K là giao của AB và CD
(1)=>góc DHK=góc KHC
=>HK là phân giác trong của góc DHC
Vì HM vuông góc HK
nên HM là phân giác góc ngoài của ΔDHC
MC/MD=HC/HD=CK/DK
CP//AD
=>CP/AD=MC/MD
CQ//AD
=>CQ/AD=CK/DK
Từ (3), (4), (5) suy ra CP/AD=CQ/AD
=>CP=CQ
=>C là trung điểm của PQ
VV
22 tháng 4 2023
vì AM là tiếp tuyến của ( O) => OA⊥AM =>ΔOAM vuông ở A
=> điểm A thuộc đường tròn đường kính OM
vì BM là tiếp tuyến của (O) => OB⊥BM =>ΔOBM vuông ở B
=> điểm B thuộc đường tròn đường kính OM
Vì OH⊥MI=>ΔOHM vuông tại H
=> điểm H thuộc đường tròn đường kính OM
=> 4 điểm O,A,M,B,H cùng thuộc đường tròn đường kính OM
12 tháng 3 2023
a:
Gọi G là giao của AE với (O)(G khác A)
góc MAE=1/2*sđ cung AG
góc MEA=1/2(sđ cung AC+sđ cung DG)
=1/2(sđ cung AC+sđ cung CG)
=1/2sđ cungAG
=góc MAE
=>ΔMAE cân tại M
=>MA=ME=MB
=>ΔMBE cân tại M
b:
Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng vơi ΔMDA
=>AC/AD=MA/MD=MC/MA
Xet ΔMBC và ΔMDB có
góc MBC=góc MDB
góc BMC chung
=>ΔMBC đồng dạng vơi ΔMDB
=>CB/DB=MB/MD=MA/MD
EC/ED=AC/AD=MA/MD=CB/BD
=>BE là phân giác của góc CBD
5 tháng 5 2022
Xét đường tròn tâm O ta có :
góc MAB = góc MCA = 1/2 sđ cung AB
Xét tam giác MAB và tam giác MCA có :
góc MAB = góc MCA
góc AMC Chung
=> \(\Delta MAB\sim\Delta MCA\)
=.> \(\dfrac{MA}{MC}=\dfrac{MB}{MA}\)
=> MA2=MC.MB
<=> 62=12.MB
=>MB =3cm
vậy MB = 3 cm
