Tìm GTNN của C = x2 + \(\dfrac{4}{x}\) và D = x + \(\dfrac{4}{x^2}\)
giúp mk vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2023
\(\dfrac{-4}{x}=\dfrac{x}{-49}\\ \Rightarrow x^2=\left(-4\right)\left(-49\right)\\ \Rightarrow x^2=196\\ \Rightarrow x=\pm14\)
\(\dfrac{3.6}{x-3}=\dfrac{5}{3}\\ \Rightarrow5\left(x-3\right)=3.3.6\\ \Rightarrow5\left(x-3\right)=54\\ \Rightarrow x-3=\dfrac{54}{5}\\ \Rightarrow x=\dfrac{54}{5}+3\\ \Rightarrow x=\dfrac{69}{15}\)
\(\left(2x+1\right):2=12:3\\ \left(2x+1\right):2=4\\2x+1=2\\ 2x=1\\ x=\dfrac{1}{2} \)
\(\left(2x-14\right):3=12:9\\ \left(2x-14\right):3=\dfrac{4}{3}\\ 2x-14=4\\ 2x=16\\ x=8\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
1.
\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{2^2}{x}+\dfrac{1}{1-x}-1\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)
\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)
2.
\(f\left(x\right)=\dfrac{1}{x}+\dfrac{1}{1-x}\ge\dfrac{4}{x+1-x}=4\)
\(f\left(x\right)_{min}=4\) khi \(x=\dfrac{1}{2}\)
11 tháng 1 2022
f(x)=4x+x−1+11−x=22x+11−x−1≥(2+1)2x+1−x−1=8f(x)=4x+x−1+11−x=22x+11−x−1≥(2+1)2x+1−x−1=8
f(x)min=8f(x)min=8 khi x=23x=23
2.
f(x)=1x+11−x≥4x+1−x=4f(x)=1x+11−x≥4x+1−x=4
f(x)min=4f(x)min=4 khi x=12
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2021
\(P=\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{x}}\Rightarrow P^2=\dfrac{x^2}{y}+\dfrac{y^2}{x}+2\sqrt{xy}\)
\(P^2=\left(\dfrac{x^2}{y}+\sqrt{xy}+\sqrt{xy}\right)+\left(\dfrac{y^2}{x}+\sqrt{xy}+\sqrt{xy}\right)-2\sqrt{xy}\)
\(P^2\ge3x+3y-2\sqrt{xy}\ge3\left(x+y\right)-\left(x+y\right)=2\left(x+y\right)=4038\)
\(\Rightarrow P\ge\sqrt{4038}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{2019}{2}\)
H
6 tháng 4 2021
Ta có:
\(P=\dfrac{x}{\sqrt{2019-x}}+\dfrac{y}{\sqrt{y-2019}}=\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{x}}\ge\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}=\sqrt{x}+\sqrt{y}\)
Lại có:
\(P=\dfrac{x}{\sqrt{2019-x}}+\dfrac{y}{\sqrt{2019-y}}=\dfrac{2019-y}{\sqrt{y}}+\dfrac{2019-x}{\sqrt{x}}\\ =\dfrac{2019}{\sqrt{x}}+\dfrac{2019}{\sqrt{y}}-\sqrt{x}-\sqrt{y}\)
\(\Rightarrow2P=\dfrac{2019}{\sqrt{x}}+\dfrac{2019}{\sqrt{y}}=2019\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\ge2019\cdot\dfrac{2}{\sqrt[4]{xy}}\\ \ge2019\dfrac{2}{\sqrt[2]{\dfrac{x+y}{2}}}=2019\cdot\dfrac{2}{\sqrt{\dfrac{2019}{2}}}=2\sqrt{2}\sqrt{2019}\)
\(\Rightarrow P\ge\sqrt{2}\sqrt{2019}\)
Dấu = khi \(x=y=\dfrac{2019}{2}\)
9 tháng 12 2021
\(1,Q=\dfrac{a^4-2a^2+a^3-2a+a^2-2}{a^4-2a^2+2a^3-4a+a^2-2}\\ Q=\dfrac{\left(a^2-2\right)\left(a^2+a+1\right)}{\left(a^2-2\right)\left(a^2+2a+1\right)}=\dfrac{a^2+a+1}{a^2+2a+1}\)
\(Q=\dfrac{x^2+x+1}{\left(x+1\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{x^2+x+1-\dfrac{3}{4}x^2-\dfrac{3}{2}x-\dfrac{3}{4}}{\left(x+1\right)^2}+\dfrac{3}{4}\\ Q=\dfrac{\dfrac{1}{4}x^2-\dfrac{1}{2}x+\dfrac{1}{4}}{\left(x+1\right)^2}+\dfrac{3}{4}=\dfrac{\dfrac{1}{4}\left(x-1\right)^2}{\left(x+1\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\\ Q_{min}=\dfrac{3}{4}\Leftrightarrow x=1\)
9 tháng 12 2021
\(2,\text{Từ GT }\Leftrightarrow\dfrac{ayz+bxz+czy}{xyz}=0\\ \Leftrightarrow ayz+bxz+czy=0\\ \text{Ta có }\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\\ \Leftrightarrow\left(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}\right)^2=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{zx}{ca}\right)=0\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\cdot\dfrac{cxy+ayz+bzx}{abc}=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\cdot\dfrac{0}{abc}=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
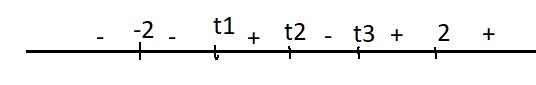
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)
Có điều kiện không bạn.