Question

[Nguyễn Châu Mỹ Linh]

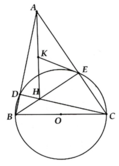
Cho tam giác nhọn ABC có \(\widehat{B}=45^o\). Vẽ đường tròn đường kính AC có tâm O, đường tròn này cắt BA và BC tại D và E

a) Chứng minh rằng AE = EB

b) Gọi H là giao điểm của CD và EA. Chứng minh rằng đường trung trực của đoạn HE đi qua điểm I của BH

c) Chứng minh BH \(\perp\) AC

Answer 1

[Nguyễn Lê Phước Thịnh]

a) Xét (O) có 

ΔAEC nội tiếp đường tròn(A,E,C cùng thuộc (O))

AC là đường kính của (O)(gt)

Do đó: ΔAEC vuông tại E(Định lí)

\(\Rightarrow\)AE\(\perp\)EC tại E

\(\Rightarrow\)AE\(\perp\)BE tại E

hay \(\widehat{AEB}=90^0\)

Xét ΔAEB có \(\widehat{AEB}=90^0\)(cmt)

nên ΔAEB vuông tại E(Định nghĩa tam giác vuông)

Xét ΔAEB vuông tại E có \(\widehat{ABE}=45^0\)(gt)

nên ΔAEB vuông cân tại E(Định lí tam giác vuông cân)

\(\Rightarrow\)AE=EB(hai cạnh bên của ΔAEB vuông cân tại E)

b)

Ta có: EA\(\perp\)EB(cmt)

nên \(EA\perp EH\) tại E

Xét ΔEHB có \(EA\perp EH\) tại E(cmt)

nên ΔEHB vuông tại E(Định nghĩa tam giác vuông)

Ta có: ΔEHB vuông tại E(cmt)

mà EI là đường trung tuyến ứng với cạnh huyền BH(I là trung điểm của BH)

nên \(EI=\dfrac{BH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

mà \(IH=BI=\dfrac{BH}{2}\)(I là trung điểm của BH)

nên EI=IH=IB

Ta có: IH=IE(cmt)

nên I nằm trên đường trung trực của HE(Tính chất đường trung trực của một đoạn thẳng)

hay đường trung trực của HE đi qua trung điểm I của BH(đpcm)

c) Ta có: \(AE\perp EC\) tại E(cmt)

nên \(AE\perp BC\) tại E

Xét (O) có 

ΔADC nội tiếp đường tròn(A,D,C cùng thuộc đường tròn(O))

AC là đường kính của (O)(gt)

Do đó: ΔADC vuông tại D(Định lí)

\(\Rightarrow CD\perp AD\) tại D

hay \(CD\perp BA\) tại D

Xét ΔBAC có 

AE là đường cao ứng với cạnh BC(cmt)

CD là đường cao ứng với cạnh BA(cmt)

AE cắt CD tại H(gt)

Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)

\(\Rightarrow\)BH là đường cao ứng với cạnh AC

hay \(BH\perp AC\)(đpcm)

Answer 2

[đình phú lưu]

 bạn ơi phần "Do đó: ΔAEC vuông tại E(Định lí)" ở câu a là định lí nào vậy?