Một bộ bài có 52 lá, hãy tính xác xuất để 2 lần xáo bài trùng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá bích n(A) = 13
Suy ra 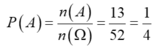
Chọn B.

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá át n(A)=4
Suy ra 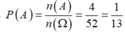
Chọn C.

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá J đỏ hay lá 5 là n(A)=2+4=6
Suy ra 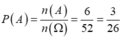
Chọn B.

Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá át hay lá rô n(A) = 4 +12 = 16.
Suy ra 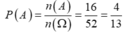
Chọn C.

Không gian mẫu: \(C_{52}^2\)
Số cách rút không có quân K nào: \(C_{48}^2\)
Xác suất: \(P=\dfrac{C_{52}^2-C_{48}^2}{C_{52}^2}=...\)

Gọi A là biến cố "Rút được 2 lá bài cơ".
Số kết quả thuận lợi là \(\left|\Omega_A\right|=C^2_{13}=78\).
Số kết quả có thể xảy ra là \(\left|\Omega\right|=C^2_{52}=1326\).
\(\Rightarrow\) Xác suất xảy ra biến cố A là \(P\left(A\right)=\dfrac{78}{1326}=\dfrac{1}{17}\).
Không gian mẫu: \(\dfrac{52!}{\left(4!\right)^{13}}\)
Do đó xác suất: \(P=\dfrac{1}{\dfrac{52!}{\left(4!\right)^{13}}}=\dfrac{\left(4!\right)^{13}}{52!}=...\)
1.
ĐKXĐ: \(-3\le x\le1\)
\(2\left(x+3\right)-m\sqrt{x+3}+5\left(1-x\right)+2m\sqrt{1-x}=4\sqrt{\left(x+3\right)\left(1-x\right)}\)
\(\Leftrightarrow m\left(2\sqrt{1-x}-\sqrt{x+3}\right)=3x-11+4\sqrt{\left(x+3\right)\left(1-x\right)}\)
Đặt \(2\sqrt{1-x}-\sqrt{x+3}=t\Rightarrow t\in\left[-2;4\right]\)
\(t^2=7-3x-4\sqrt{\left(1-x\right)\left(x+3\right)}\)
\(\Rightarrow3x-11+4\sqrt{\left(1-x\right)\left(x+3\right)}=-4-t^2\)
Do đó pt trở thành: \(m.t=-t^2-4\)
- Với \(t=0\) ko phải nghiệm
- Với \(t\ne0\Rightarrow m=\dfrac{-t^2-4}{t}\)
Xét \(f\left(t\right)=\dfrac{-t^2-4}{t}\) với \(t\in\left[-2;4\right]\)
\(f^2\left(t\right)=\dfrac{\left(t^2+4\right)^2}{t^2}\ge4\Rightarrow\left[{}\begin{matrix}f\left(t\right)\le-2\\f\left(t\right)\ge2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\le-2\\m\ge2\end{matrix}\right.\)