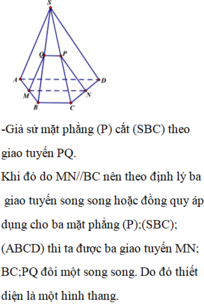
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB//CD, AB=2CD. Các cạnh bên có độ dài = 1. Gọi O là giao điểm của AC và BD. I là trung điểm của SO. Mặt phẳng \(\left(\alpha\right)\) thay đổi đi qua I và cắt SA,SB,SC,SD lần lượt tại M,N,P,Q. Tìm GTNN của biểu thức \(T=\dfrac{1}{2SM^2}+\dfrac{1}{2SN^2}+\dfrac{1}{SP^2}+\dfrac{1}{SQ^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

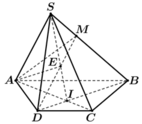
Ta có A là điểm chung thứ nhất.
Gọi 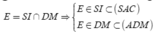
=> E là điểm chung thứ hai.
Vậy AE là giao tuyến của (ADM) và (SAC)
Chọn B.

D là đáp án đúng (do I là giao điểm AC và BM \(\Rightarrow I=\left(SAC\right)\cap\left(SBM\right)\)
\(\Rightarrow SI=\left(SAC\right)\cap\left(SBM\right)\)

Chọn C
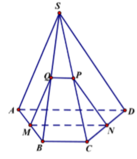
Giả sử mặt phẳng (P) cắt (SBC) theo giao tuyến PQ. Khi đo đó MN//BC nên theo định lý ba giao tuyến song song hoặc đồng quy áp dụng cho ba mặt phẳng (P);(SBC);(ABCD) thì ta được ba giao tuyến MN;BC;PQ đôi một song song. Do đó thiết diện là một hình thang.

Chọn C
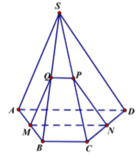
Giả sử mặt phẳng (P) cắt (SBC) theo giao tuyến PQ. Khi đo đó MN//BC nên theo định lý ba giao tuyến song song hoặc đồng quy áp dụng cho ba mặt phẳng (P);(SBC);(ABCD) thì ta được ba giao tuyến MN;BC;PQ đôi một song song. Do đó thiết diện là một hình thang.