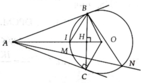
Cho đường tròn (O) và một điểm A nằm ngoài dường tron (O). Qua A vẽ các tiếp tuyến AB, AC với đường tron (O) (B,C là các tiếp điểm), AO cắt BC tại D.
a) Chứng minh \(\Delta ABC\)cân tại A và AO là đường trung trực của BC
b) Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh: \(\Delta AGO\approx\Delta HDO\)(hai tam giác đồng dạng)
c) Chứng minh EH là tiếp tuyến của đường tròn (O)