m2 + 4mx + 16 = m2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Vì $\Delta'=(-2m)^2-(m^2-5)=3m^2+5>0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm pb với mọi $m\in\mathbb{R}$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm thì:
$x_1+x_2=4m$
$x_1x_2=m^2-5$
Khi đó:
$A=2(x_1-x_2)^2=2[(x_1+x_2)^2-4x_1x_2]=2[(4m)^2-4(m^2-5)]=2(12m^2+20)$
$=24m^2+40$
Δ=(-4m)^2-4(m^2-5)
=16m^2-4m^2+20=12m^2+20>=0
=>Phương trình luôn có hai nghiệm
A=2[(x1+x2)^2-4x1x2]
=2[(4m)^2-4(m^2-5)]
=2[16m^2-4m^2+20]
=24m^2+40

\(c,PT\Leftrightarrow m^2x-9x-\left(m^2-4m+3\right)=0\\ \Leftrightarrow x\left(m^2-9\right)-\left(m-3\right)\left(m-1\right)=0\)
PT có nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-9=0\\\left(m-3\right)\left(m-1\right)=0\end{matrix}\right.\Leftrightarrow m=3\)
\(d,PT\Leftrightarrow m^2x-m^2-4mx+5m-4=0\\ \Leftrightarrow x\left(m^2-4m\right)-\left(m^2-5m+4\right)=0\\ \Leftrightarrow xm\left(m-4\right)-\left(m-1\right)\left(m-4\right)=0\)
PT có nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m\left(m-4\right)=0\\\left(m-4\right)\left(m-1\right)=0\end{matrix}\right.\Leftrightarrow m=4\)

a) 4 m2 = 40000 cm2 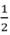 m2 = 50dm2
m2 = 50dm2
16 m2 = 1600 dm2 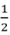 dm2 = 50 cm2
dm2 = 50 cm2
308 dm2 = 30800cm2 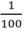 m2 = 100 cm2
m2 = 100 cm2
b) 700 cm2 = 7 dm2 15 m2 9 dm2 = 1509 dm2
3400 dm2 = 34 m2 7 dm2 25 cm2 = 725 cm2
50 000 cm2 = 5 m2 28 m2 50 cm2 = 280050 cm2
c) 948 dm2 = 9 m2 48 dm2 8791 dm2 = 87 m2 91 dm2
705 cm2 = 7 dm2 5cm2 30 045 cm2 = 3 m2 45 cm2
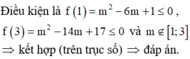



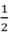 m2 = ……dm2
m2 = ……dm2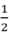 dm2 = …… cm2
dm2 = …… cm2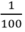 m2 = …… cm2
m2 = …… cm2