tim giá trị x,y (x là số nguyên tố) biết :
x2-6xy+9y2-3x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DK
1
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
$A=(x-3y)^2-15=[37-3(-1)]^2-15=40^2-15=1585$
25 tháng 10 2021
Câu 1 Thực hiện phép tính :
a) 2x( 3x2 - 4x + 2 )
b) 2x( 3x + 5 ) - 3 ( 2x2 - 2x + 3 )
GIẢI GIÙM EM ĐC KO Ạ
VH
0
CM
16 tháng 8 2017
Đáp án A.
Ta có x2 + 9y2 = 6xy <=> (x – 3y)2 = 0 <=> x = 3y.
⇒ M = 1 + log 12 x + log 12 y 2 . log 12 6 y = log 12 12 + log 12 3 y 2 log 12 36 y 2
= log 12 36 y 2 log 12 36 y 2 = 1 .
CM
2 tháng 1 2018
Chọn B.
Ta có x2 + 9y2 = 6xy tương đương (x - 3y) 2 = 0 hay x = 3y.
Khi đó 
21 tháng 10 2021
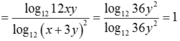
a: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1+4-2\left(4x^2-12x+9\right)\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
e: \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)=8x^3+27y^3\)
2 tháng 10 2021
\(A=x^3-8-128-x^3=-136\\ B=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)
2 tháng 10 2021
\(A=\left(x-2\right)\left(x^2+2x+4\right)-\left(128+x^3\right)=x^3-8-128-x^3=-136\)
\(B=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)-\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)
TP
3 tháng 11 2015
vì x+y=4 nền (x+y)^2=4^2 =x^2+ 2xy+y^2=16 ma xy=5 nên 2xy=10 ta có x^2+y^2+10=16 ; x^2+y^2= 16-10 x^2+y^2=6 kết quả mik là z đó nhưng k biết có đúng k bn ak
Ta có \(x^2-6xy+9y^2-3x=0\left(1\right)\)
\(\Leftrightarrow3x=\left(x-3y\right)^2⋮3\Rightarrow3x=\left(x-3y\right)^2⋮9\)
\(\Rightarrow x⋮3\)
Mà \(x\) là số nguyên tố nên \(x=3\)
\(\left(1\right)\Leftrightarrow3x=\left(x-3y\right)^2\)
\(\Leftrightarrow9=\left(9-3y\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}y=2\\y=4\end{matrix}\right.\)
Thử lại được \(x=3;y=2\)
hôm qua mình thi hsg câu này mà ko bt làm