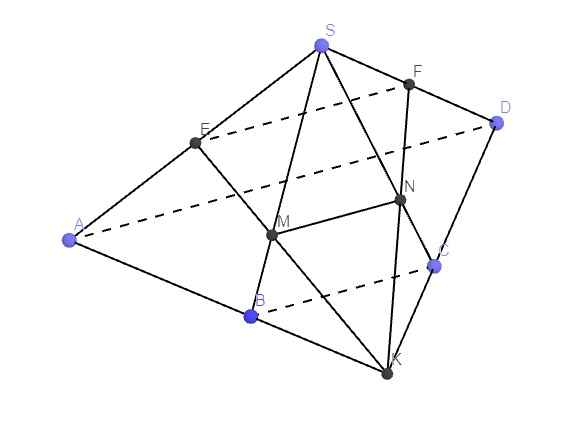
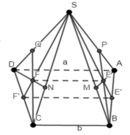
Cho hình chóp S.ABCD có đáy là hình thang (AD//BC,AD>BC). Gọi M,N,E lần lượt là trung điểm của AB,CD,SA .
a) Chứng minh rằng : (MEN) // (SBC)
b) Trong tam giác SAD vẽ EF // AD (F\(\in\) SD) . Chứng minh rằng F là giao điểm của mặt phẳng (MNE) với SD . Từ đó suy ra thiết diện của hình chóp khi cắt bởi mặt phẳng (MNE) là hình gì ?

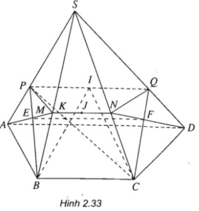
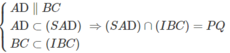
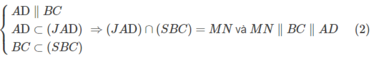
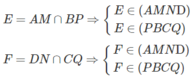
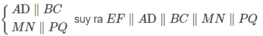
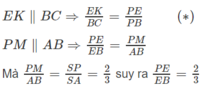
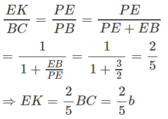
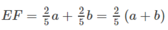


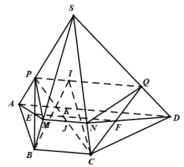

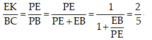
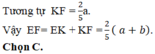
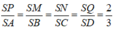

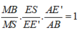
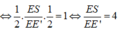
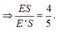
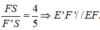
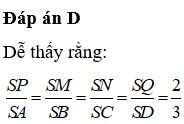


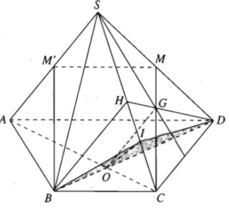
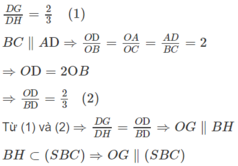


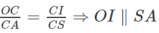
Cho tứ diện ABCD . Gọi G1,G2,G3 lần lượt là trọng tâm của các tam giác ABC,ACD,ABD . Chứng minh mặt phẳng (G1G2G3) // (BCD)