Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

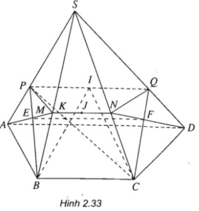
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy
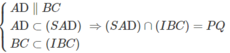
Và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy
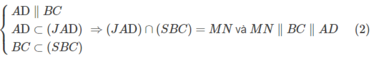
Từ (1) và (2) suy ra PQ // MN.
b) Ta có:
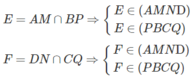
Do đó: EF = (AMND) ∩ (PBCQ)
Mà
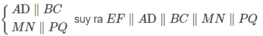
Tính
EF: CP ∩ EF = K ⇒ EF = EK + KF
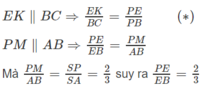
Từ (∗) suy ra
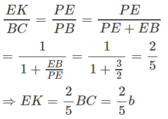
Tương tự ta tính được KF = 2a/5
Vậy: 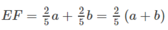

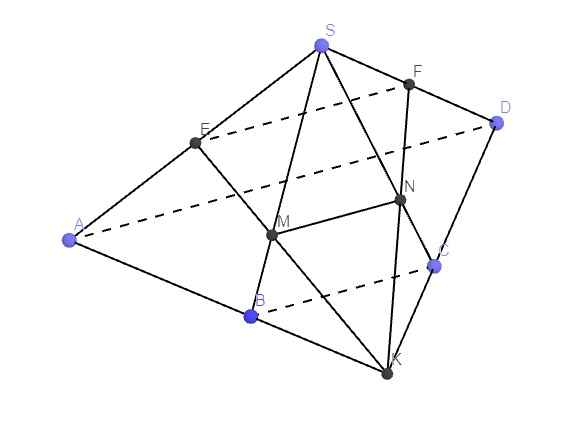
Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)

Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
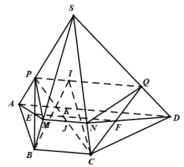
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp

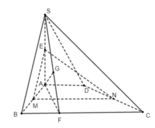
+ Ta có: M N // B C ⇒ M N // S B C E M // S B ⇒ E M // S B C ⇒ M N E // S B C
⇒ d((MNE); (SBC)) = d(M; (SBC))
+ Lại có: AM ∩ (SBC) = B ⇒ d A ; S B C d M ; S B C = A B M B = 2 ⇒ d(M; (SBC)) = 1/2 d(A;(SBC))
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC))
+ Từ A hạ AF ⊥ BC tại F, AG ⊥ SF tại G
B C ⊥ S A B C ⊥ A F ⇒ B C ⊥ S A F ⇒ B C ⊥ A G mà AG ⊥ SF nên AG ⊥ (SBC)
⇒ d(A;(SBC)) = AG
+ Tính AG
Do ABCD là hình thang cân, BC = 2a nên suy ra BF = a/2
⇒ AF = BF. tan 60 ° = a 3 2
Tam giác SAF vuông tại A có AG là đường cao
⇒ 1 A G 2 = 1 S A 2 + 1 A F 2 ⇒ AG = a 66 11
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC)) = 1/2 AG = a 66 22 .
Đáp án C



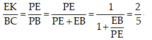
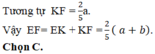
Cho tứ diện ABCD . Gọi G1,G2,G3 lần lượt là trọng tâm của các tam giác ABC,ACD,ABD . Chứng minh mặt phẳng (G1G2G3) // (BCD)