Có bạn nói rằng các phân thức 2 x 2 x - 2 ; 1 x 2 - 2 x + 1 ; 5 x 3 x - 1 x 2 + 1 có cùng điều kiện biến x. Điều đó đúng hay sai? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2017
Phân thức: \(\dfrac{2x}{2x-2}\)
ĐKXĐ: \(x\ne1\)
Phân thức: \(\dfrac{1}{x^2-2x+1}=\dfrac{1}{\left(x-1\right)^2}\)
ĐKXĐ: \(x\ne1\)
Phân thức: \(\dfrac{5x^3}{\left(x-1\right)\left(x^2+1\right)}\)
ĐKXĐ: \(x\ne1\)
Vậy các phân thức : \(\dfrac{2x}{2x-2};\dfrac{1}{x^2-2x+1};\dfrac{5x^3}{\left(x-1\right)\left(x^2+1\right)}\)
có cùng điều kiện của biến x là \(x\ne1\)
29 tháng 6 2017
\(2x-2\ne0\) khi \(x\ne1;x^2-2x+1=\left(x-1\right)^2\ne0\) khi \(x\ne1,\left(x-1\right)\left(x^2+1\right)\ne0\) khi \(x\ne1\). Vậy biến \(x\) trong ba phân thức này có cùng một điều kiện \(x\ne1\) là đúng.
20 tháng 12 2019
\(A=\frac{1}{x-2}+\frac{1}{x-2}+\frac{x^2+1}{x^2-4}\)
a)\(A=\frac{1}{x-2}+\frac{1}{x-2}+\frac{x^2+1}{x^2-4}\)
\(=\frac{x-2+x-2}{x^2-4}+\frac{x^2+1}{x^2-4}\)
\(=\frac{x^2+2x-3}{x^2-4}\)
đầu bài sai rồi bạn ơi bạn cho x=0 thì \(A=\frac{3}{4}\)là số dương rồi
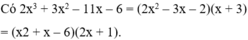
Ta có: 2 x 2 x - 2 xác định khi 2x – 2 ≠ 0 ⇒ 2x ≠ 2 ⇒ x ≠ 1
1 x 2 - 2 x + 1 = 1 x - 1 2 xác định khi x - 1 2 ≠ 0 ⇒ x – 1 ≠ 0 ⇒ x ≠ 1
5 x 3 x - 1 x 2 + 1 xác định khi x - 1 x 2 + 1 ≠ 0 hay x – 1 ≠ 0
( vì với mọi x thì x 2 ≥ 0 nên x 2 + 1 > 0 )
Do đó, phân thức 5 x 3 x - 1 x 2 + 1 xác định với x ≠ 1.
Vậy các phân thức 2 x 2 x - 2 ; 1 x 2 - 2 x + 1 ; 5 x 3 x - 1 x 2 + 1 có cùng điều kiện biến x là đúng.