Tìm các số nguyên a và b thoả mãn: |a| + |b| = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
n4 + 4 = n4 + 4n2 + 4 – 4n2
= (n2 + 2 )2 – (2n)2
= (n2 + 2 – 2n )(n2 + 2 + 2n)
Vì n4 + 4 là số nguyên tố nên n2 + 2 – 2n = 1 hoặc n2 + 2 + 2n = 1
Mà n2 + 2 + 2n > 1 vậy n2 + 2 – 2n = 1 suy ra n = 1
Thử lại : n = 1 thì 14 + 4 = 5 là số nguyên tố
Vậy với n = 1 thì n4 + 4 là số nguyên tố.

Giải : Xét phép trừ thứ nhất : Ở cột hàng trăm ta có a \(\ge\) c nên phép trừ ở hàng đơn vị và hàng chục có nhớ . Do đó ở cột hàng trăm :
a - c - 1 ( nhớ ) = 0 \(\Rightarrow\) c = a - 1 (1)
Xét phép trừ thứ hai : Ở cột hàng trăm ta có b > a nên phép trừ ở hàng chục có nhớ . Do đó ở cột hàng trăm :
b - a - 1 ( nhớ ) = 2 \(\Rightarrow\) a = b - 3 (2)
Từ (1) và (2) suy ra : c = b - 4 (3)
Từ (2) và (3) suy ra :
a + b + c = ( b - 3 ) + b + ( b - 4 ) = 3b - 7 \(\le\) 20.
Số không quá 20 và là tổng của bốn số chẵn liên tiếp có thể bằng :
0 + 2 + 4 + 6 = 12 hoặc 2 + 4 + 6 + 8 = 20.
Trường hợp 3b - 7 = 12 cho 3b = 19 , loại .
Trường hợp 3b - 7 = 20 cho 3b = 27 nên b = 9.
Từ đó : a = 9 - 3 = 6 ; c = 9 - 4 = 5.
Ta được :
695 - 596 = 99
965 - 695 = 270

Không tồn tại a b c thỏa mãn đề
Do vế sau có ab*ac*7 = a^2*100*7 +... trong khi vế trước hàng trăm chỉ có a mà vế sau hàng trăm lên tới lớn hoặc bằng a^2*7 nên đăng thức không thể tòn tại
tick nha nếu đúng

x + 4 \(⋮\) x + 1
x + 1 + 3 \(⋮\) x + 1
Mà x+ 1 \(⋮\) x + 1
=> 3 \(⋮\) x + 1
=> x + 1 \(\in\) Ư ( 3 )
=> x + 1 \(\in\) { 1 , 3 }
=> x \(\in\) { 0 , 2 }
\(a)x+4⋮x+1\)
\(\Rightarrow x+1+3⋮x+1\)
Mà x + 1 \(⋮\)x + 1 => x + 1 \(\inƯ(3)=\left\{\pm1;\pm3\right\}\)
Lập bảng :
| x + 1 | 1 | -1 | 3 | -3 |
| x | 0 | -2 | 2 | -4 |
Vậy \(x\in\left\{0;-2;2;-4\right\}\)
Câu b tự làm
Tk mk nhé

a. Các số nguyên x thỏa mãn là : -9 ; - 8 ; - 7 ; ...... ; 13 ; 14
b. Tổng của chúng là :
-9 - 8 - 7 - 6 -... - 1 + 0 + 1 + ... + 13 = 10 +... + 13
= 46
a ) Tâất cả các số nguyên vừa tìm đc là :
-9 ; - 8 ; -7 ;.....-1 ; 0 ; 1 ;.............14
b ) Tất cả tổng vừa tìm đc là :
( -9 + 9 ) + ( -8 + 8 ) + ............+ 0 + 10 + 11 + 12 + 13 + 14
= 0 + 0 + .......+ 0 + 10 + 11 + 12 + 13 + 14
= 60

Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), tức là x + 1 là ước của 3.
Vì Ư(3) = {-1; 1; -3; 3} ta có bảng sau:

Đáp số x = -4; -2; 0; 2.

Ta có 4x + 3 = 4(x - 2) + 11
nên (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), tức là x -2 là ước của 11
Ư(11) = { -11; -1; 1; 11}; ta có bảng sau:
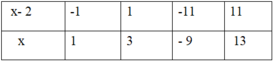
Vậy các số nguyên x thỏa mãn là: x ∈ { 1; 3; - 9; 13}

Các số nguyên x thỏa mãn -10 < x < 15 là:
x ∈ { -9; -8; -7; ...; -1; 0; 1; 2; ...; 13; 14}
Cách 1: Giá trị tuyệt đối của một số nguyên là một số tự nhiên và tổng hai số tự nhiên bằng 0 khi cả hai số đó đều bằng 0. Nên a = 0 và b = 0.
Cách 2: Vì |a| ≥ 0 và |b|≥ 0| nên |a| + |b| ≥ 0
Vì vậy |a| + |b| = 0 khi |a| = |b| = 0 hay a = b = 0.