Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các số nguyên x thỏa mãn -10 < x < 15 là:
x ∈ { -9; -8; -7; ...; -1; 0; 1; 2; ...; 13; 14}

Ta có
n4 + 4 = n4 + 4n2 + 4 – 4n2
= (n2 + 2 )2 – (2n)2
= (n2 + 2 – 2n )(n2 + 2 + 2n)
Vì n4 + 4 là số nguyên tố nên n2 + 2 – 2n = 1 hoặc n2 + 2 + 2n = 1
Mà n2 + 2 + 2n > 1 vậy n2 + 2 – 2n = 1 suy ra n = 1
Thử lại : n = 1 thì 14 + 4 = 5 là số nguyên tố
Vậy với n = 1 thì n4 + 4 là số nguyên tố.



Ta có: abc < ab+bc+ca
\(\Rightarrow\frac{ab+bc+ca}{abc}>\frac{abc}{abc}\)
\(\Rightarrow\frac{ab}{abc}+\frac{bc}{abc}+\frac{ca}{abc}>1\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}>1\)
Vì a,b,c có vai trò như nhau . Nếu giả sử a>b>c
\(\Rightarrow\frac{1}{a}< \frac{1}{b}< \frac{1}{c}\Rightarrow1< \frac{1}{c}+\frac{1}{a}+\frac{1}{b}< \frac{3}{c}\)
\(\Rightarrow1< \frac{3}{c}\)
\(\Rightarrow c>3\) mà c là SNT \(\Rightarrow c=2\left(1\right)\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}>1-\frac{1}{2}=\frac{1}{2}\)
\(\Rightarrow b>2\). Giả sử b > 3
\(\frac{1}{b}< \frac{1}{3}\left(2\right)\)mà \(\frac{1}{a}< \frac{1}{b}\)
\(\Rightarrow\frac{1}{a}< \frac{1}{3}\)
Kết hợp (2) \(\Rightarrow\frac{1}{a}+\frac{1}{b}< \frac{1}{3}+\frac{1}{3}=\frac{2}{3}\)mà \(\frac{2}{3}>\frac{1}{2}\)
\(\Rightarrow\) giả sử sai
\(\Rightarrow b< 3\)mà \(b\ne c\Rightarrow b\ne2\)và b là SNT
\(\Rightarrow b=3\left(3\right)\)
\(\Rightarrow\frac{1}{a}>\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\)
\(\Rightarrow a< 6\)mà \(a>b;b=3;b\ne a\)
\(\Rightarrow3< a< 6\)mà a là SNT
\(\Rightarrow a=5\left(4\right)\)
Mà a,b,c vai trò như nhau
Kết hợp (1) , (3) , (4) \(\Rightarrow\left(a,b,c\right)\in\left\{\left(2,3,5\right);\left(5,3,2\right);\left(3,2,5\right);\left(5,2,3\right);\left(2,5,3\right);\left(3,5,2\right)\right\}\)( tm điều kiện )
Mn tham khảo nhé

Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), tức là x + 1 là ước của 3.
Vì Ư(3) = {-1; 1; -3; 3} ta có bảng sau:

Đáp số x = -4; -2; 0; 2.

Ta có 4x + 3 = 4(x - 2) + 11
nên (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), tức là x -2 là ước của 11
Ư(11) = { -11; -1; 1; 11}; ta có bảng sau:
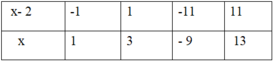
Vậy các số nguyên x thỏa mãn là: x ∈ { 1; 3; - 9; 13}

Cách 1: Giá trị tuyệt đối của một số nguyên là một số tự nhiên và tổng hai số tự nhiên bằng 0 khi cả hai số đó đều bằng 0. Nên a = 0 và b = 0.
Cách 2: Vì |a| ≥ 0 và |b|≥ 0| nên |a| + |b| ≥ 0
Vì vậy |a| + |b| = 0 khi |a| = |b| = 0 hay a = b = 0.

x + 4 \(⋮\) x + 1
x + 1 + 3 \(⋮\) x + 1
Mà x+ 1 \(⋮\) x + 1
=> 3 \(⋮\) x + 1
=> x + 1 \(\in\) Ư ( 3 )
=> x + 1 \(\in\) { 1 , 3 }
=> x \(\in\) { 0 , 2 }
\(a)x+4⋮x+1\)
\(\Rightarrow x+1+3⋮x+1\)
Mà x + 1 \(⋮\)x + 1 => x + 1 \(\inƯ(3)=\left\{\pm1;\pm3\right\}\)
Lập bảng :
| x + 1 | 1 | -1 | 3 | -3 |
| x | 0 | -2 | 2 | -4 |
Vậy \(x\in\left\{0;-2;2;-4\right\}\)
Câu b tự làm
Tk mk nhé
a. Các số nguyên x thỏa mãn là : -9 ; - 8 ; - 7 ; ...... ; 13 ; 14
b. Tổng của chúng là :
-9 - 8 - 7 - 6 -... - 1 + 0 + 1 + ... + 13 = 10 +... + 13
= 46
a ) Tâất cả các số nguyên vừa tìm đc là :
-9 ; - 8 ; -7 ;.....-1 ; 0 ; 1 ;.............14
b ) Tất cả tổng vừa tìm đc là :
( -9 + 9 ) + ( -8 + 8 ) + ............+ 0 + 10 + 11 + 12 + 13 + 14
= 0 + 0 + .......+ 0 + 10 + 11 + 12 + 13 + 14
= 60