Gọi α là mặt phẳng đi qua M 1 ; − 1 ; 2 và chứa trục Ox. Điểm nào trong các điểm sau đây thuộc mặt phẳng α ?
A. M 0 ; 4 ; − 2 .
B. N 2 ; 2 ; − 4 .
C. P − 2 ; 2 ; 4 .
D. Q 0 ; 4 ; 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT nên có phương trình:
6(x - 1) - 5(y+3)+(z - 4)=0
→ 6x - 5y + z - 25 = 0

Đáp án B.
Phương pháp: Mặt phẳng α đi qua M và nhận
![]()
Cách giải: Mặt phẳng α đi qua M và nhận là 1 VTPT nên có phương trình:
![]()
nên có phương trình:
![]()
![]()

Đáp án B.
Phương pháp: Mặt phẳng α đi qua M
![]()
Cách giải: Mặt phẳng α đi qua M và
![]()
nên có phương trình:
![]()
![]()

Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT nên có phương trình:
6(x– 1) + 2(y+3) – (z– 4) = 0 → 6x + 2y – z +4 = 0

Ta có ![]() mặt phẳng (P) có VTPT
mặt phẳng (P) có VTPT ![]()
Suy ra ![]()
Mặt phẳng
α
đi qua P(2;0;-1) và nhận ![]() làm một VTPT nên có phương trình
α
: -7x + 11y + z + 15 = 0
làm một VTPT nên có phương trình
α
: -7x + 11y + z + 15 = 0
Chọn C.

Đáp án A
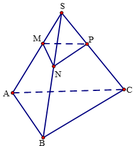
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2
Đáp án B.
Phương pháp:
Mặt phẳng α nhận i → 1 ; 0 ; 0 , O M → = 1 ; − 1 ; 2 là cặp vecto chỉ phương ⇒ n → = i → ; O M → là một vecto pháp tuyến của α
Cách giải:
α là mặt phẳng đi qua M 1 ; − 1 ; 2 và chứa trục Ox ⇒ α nhận i → 1 ; 0 ; 0 , O M → = 1 ; − 1 ; 2 là cặp vecto chỉ phương ⇒ n → = i → ; O M → = 0 ; − 2 ; − 1 là một vecto pháp tuyến của α .
α : 0. x − 0 − 2. y − 0 − 1 z − 0 = 0 ⇔ 2 y + z = 0
Dễ dàng kiểm tra N 2 ; 2 ; − 4 ∈ α