Cho mặt trụ (T) và một điểm S cố định nằm ngoài (T). Một đường thẳng
Δ
luôn đi qua S và cắt (T) tại hai điểm A, B (A, B có thể trùng nhau). Gọi M là trung điểm của đoạn thẳng AB. Tập hợp các điểm M là A. Một mặt phẳng đi qua S. B. Một mặt cầu đi qua S. C. Một mặt nón có đỉnh là S. D. Một mặt...
Đọc tiếp
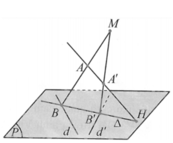
Cho mặt trụ (T) và một điểm S cố định nằm ngoài (T). Một đường thẳng Δ luôn đi qua S và cắt (T) tại hai điểm A, B (A, B có thể trùng nhau). Gọi M là trung điểm của đoạn thẳng AB. Tập hợp các điểm M là
A. Một mặt phẳng đi qua S.
B. Một mặt cầu đi qua S.
C. Một mặt nón có đỉnh là S.
D. Một mặt trụ.
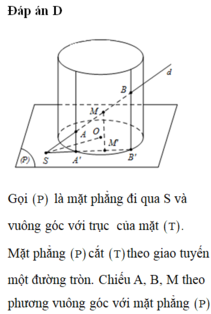
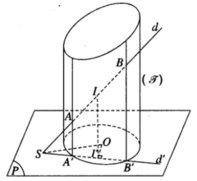
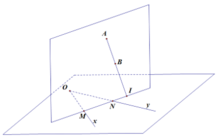
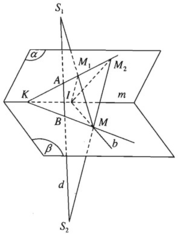
Đáp án D
Gọi P là mặt phẳng đi qua S và vuông góc với trục của mặt T . Mặt phẳng P cắt T theo giao tuyến một đường tròn. Chiếu A, B, M theo phương vuông góc với mặt phẳng P ta được các điểm theo thứ tự là A ' , B ' , M ' thẳng hàng với S, trong đó A’,B’ nằm trên đường tròn tâm O trong mặt phẳng P và M’là trung điểm của A’B’. Do đó M’ luôn nằm trên đường tròn đường kính SO trong mặt phẳng P và MM’ vuông góc với P . Vậy MM’ nằm trên mặt trụ T ' chứa đường tròn đường kính SO và có trục song song với trục của mặt trụ T .