Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

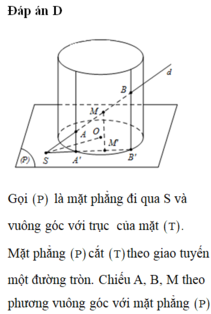
Gọi (P) là mặt phẳng đi qua S và vuông góc với trục của mặt trụ ( J ). Mặt phẳng (P) cắt ( J ) theo một đường tròn tâm O. Ta hãy xét một vị trí của đường thẳng d. Gọi A, B là giao điểm của d với ( J ) và I là trung điểm của đoạn AB. Chiếu A, B, I theo phương vuông góc với mặt phẳng (P) ta được các điểm theo thứ tự là A’ , B’ , I’ thẳng hàng với S, trong đó A’, B’ nằm trên đường tròn tâm O trong mặt phẳng (P) và I’ là trung điểm của đoạn A’B’. Do đó điểm I’ luôn luôn nằm trên đường tròn đường kính SO trong mặt phẳng (P) và đường thẳng II’ vuông góc với (P). Ta suy ra đường thẳng II’ nằm trên mặt trụ ( J ′) chứa đường tròn đường kính SO nằm trong (P) và có trục song song với trục của mặt trụ ( J ) .
Tất nhiên, điểm I chỉ nằm trong phần mặt trụ ( J ′) thuộc miền trong của mặt trụ ( J )

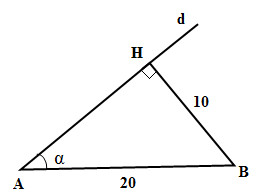
Từ B vẽ đường thẳng vuông góc với d và cắt d tại H.
Ta có BH = 10cm = d(B,d)
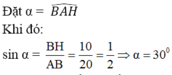
Vậy đường thẳng d nằm trên mặt nón có đỉnh là A, trục là đường thẳng AB và góc ở đỉnh là 2α = 60 °

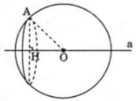
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

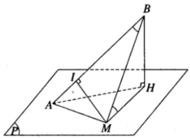
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau. Do đó MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.

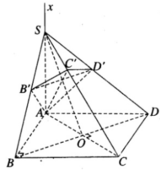
Ta có
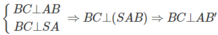
Ta lại có AB′ ⊥ SC nên suy ra AB′ ⊥ (SBC). Do đó AB′ ⊥ B′C
Chứng minh tương tự ta có AD′ ⊥ D′C.
Vậy ∠ ABC = ∠ AB′C = ∠ AC′C = ∠ AD′C = ∠ ADC = 90 °
Từ đó suy ra 7 điểm A, B, C, D, B’, C’, D’ cùng nằm trên mặt cầu đường kính là AC.

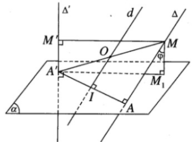
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.