Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
Hỗn hợp 5,8 gam có M (a mol) và M2Ox (b mol) Þ Ma + (2M + 16x).b = 5,8 (1)
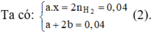
Với x = 1 hoặc 2 thay vào (1), (2) suy ra M = 137 (Ba)
Giả sử M có hóa trị n duy nhất.
⇒ CT oxit của M là M2On.
PT: \(2M+2nH_2O\rightarrow2M\left(OH\right)_n+nH_2\)
\(M_2O_n+nH_2O\rightarrow2M\left(OH\right)_n\)
Ta có: \(n_{H_2}=0,01\left(mol\right)\) và \(n_{M\left(OH\right)_n}=0,02\left(mol\right)\)
Giả sử: \(\left\{{}\begin{matrix}n_M=a\left(mol\right)\\n_{M_2O_n}=b\left(mol\right)\end{matrix}\right.\)
⇒ \(a=\dfrac{0,02}{n}\left(mol\right)\)
và \(n_{M\left(OH\right)_n}=a+2b=0,02\Rightarrow b=0,01-\dfrac{0,01}{n}\left(mol\right)\)
Mà: mM + mM2On = 2,9
\(\Rightarrow aM_M+b\left(2M_M+16n\right)=2,9\)
\(\Rightarrow M_M\left(a+2b\right)=2,9-16nb\)
\(\Rightarrow0,02M_M=2,9-16n\left(0,01-\dfrac{0,01}{n}\right)\)
\(\Rightarrow M_M=153-8n\)
Với n = 1 ⇒ MM = 145 (loại)
n = 2 ⇒ MM = 137 (nhận)
Vậy: M là Ba.
Bạn tham khảo nhé!
\(\Rightarrow\)
Đáp án C
M : x mol ; M2On : y mol
M + H2O → M(OH)n + n/2 H2
x x n 2 x
=> n 2 x = 0,01 => nx = 0,02
M2On + nH2O →2M(OH)n
y 2y
⇒ n M(OH)n = x + 2y = 0,02
+) n = 1 (KL kiềm ) ⇒x = 0,02 ; y = 0 ⇒ B. loại
+) n = 2 (KL kiềm thổ) ⇒ x = 0,01 , y = 0,05
⇒ mhh = 0,01.M + 0,05.(2M + 16.2) = 2,9
⇒ M = Ba
Đáp án B
M : x mol ; M2On : y mol
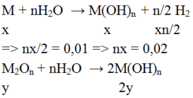
⇒ n M(OH)n = x + 2y = 0,02
+) n = 1 (KL kiềm ) ⇒ x = 0,02 ; y = 0 ⇒ loại
+) n = 2 (KL kiềm thổ) ⇒ x = 0,01 , y = 0,005
⇒ mhh = 0,01.M + 0,005.(2M + 16.2) = 2,9
⇒ M = Ba
Gọi n có hóa trị là n -> oxit của R là R2On.
Vì R tác dụng được với H2O nên n=1 hoặc 2.
Phản ứng:
\(2R+2nH_2O\) → 2\(R\)(\(OH\))\(_n\)+\(nH_2\)
\(R_2O_n+_{ }nH_2O\)→\(2R\left(OH\right)_n\)
Ta có:
\(^nH2=\dfrac{1,12}{22,4}=0,05\left(mol\right)\)
\(^nR=\dfrac{2nH2}{n}=\dfrac{0,1}{n}\)
Chất tan là R(OH)n
\(^nR\left(OH\right)n0,25.0,5=0,125\left(mol\right)=^nR+^{2n}R2On=\dfrac{0,125-\dfrac{0,1}{n}}{2}=0,0625-\dfrac{0,05}{n}\)
⇒\(\dfrac{0,1}{n}.R+\left(0,0625-\dfrac{0,05}{n}\right).\left(2R+16n\right)=18,325\)
Thay \(n\) bằng 1 và 2 thì thỏa mãn \(n\)= 2 thì \(R\) = 137 thỏa mãn \(R\) là \(Ba\).
