Tìm tất cả các giá trị của tham số m để đường thẳng y = ( m - 1 ) x cắt đồ thị hàm số y = x 3 - 3 x 2 + m + 1 tại 3 điểm phân biệt A, B, C sao cho AB=BC
A. m ∈ ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ )
B. m ∈ ( - 5 4 ; + ∞ )
C. m ∈ ( - 2 ; + ∞ )
D. m ∈ ℝ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
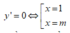
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
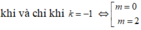

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
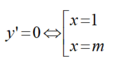
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 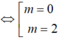
Chọn C.

Đáp án là B.
Phương trình hoàng độ giao điểm của
C & d : x + m 2 x − 1 = − x + 1 ; x ≠ 1 2
⇔ 2 x 2 + 2 m x − m − 1 = 0 (1)
C & d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .
Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0 ⇔ m ∈ ℝ .
Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC