

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
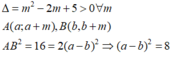
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3

Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC

Đáp án C
Điều kiện: x≠2.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình
2 x x − 2 = x + m ⇔ 2 x x − 2 − x − m = 0 ⇔ 2 x − x 2 + 2 x − m x + 2 m x − 4 = 0 ⇔ − x 2 + 4 − m x + 2 m x − 2 = 0.
Để hai đồ thị hàm số giao nhau tại hai điểm phân biệt A,B ta có
4 − m 2 + 8 m > 0 g 2 ≠ 0 ⇔ m 2 + 16 > 0 − 4 + 8 − 2 m + 2 m ≠ 0
thỏa mãn với mọi m ∈ ℝ .
Theo bài ra ta có x A + x B + x O = 3 x A + m + x B + m + y O = 7 ⇔ 4 − m = 3 4 − m + 2 m = 5 ⇔ m = 1 .
Vậy m=1 thỏa mãn điều kiện đề bài.

Đáp án là B.
Phương trình hoàng độ giao điểm của
C & d : x + m 2 x − 1 = − x + 1 ; x ≠ 1 2
⇔ 2 x 2 + 2 m x − m − 1 = 0 (1)
C & d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .
Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0 ⇔ m ∈ ℝ .

Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1