Trong thí nghiệm Yang về giao thoa ánh sáng, khe S được chiếu đồng thời hai ánh sáng đơn sắc có bước sóng λ1 = 0,48µm và λ2 là ánh sáng đơn sắc màu cam (có dải bước sóng từ 0,59 μm đến 0,65 μm). Trên màn quan sát, giữa hai vân sáng liên tiếp trùng màu với vân trung tâm có 3 vân màu cam. Giá trị λ2 bằng
A. 0,60 µm
B. 0,64 µm
C. 0,62 µm
D. 0,65 µm





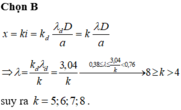
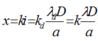

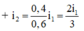
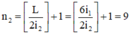

Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
Giữa hai vân trùng màu với vân trung tâm có 3 vân sáng màu cam, chứng tỏ rằng vị trí trùng nhau gần nhất của hai bức xạ ứng với vân sáng bậc 4 của bức xạ cam
+ Từ điều kiện trùng nhau của hai hệ vân ta có:
Chọn A