Hình thang ABCD (BC// AD) có ∠ C = 3 ∠ D. Khẳng định nào dưới đây là đúng ?
A. ∠ (A ) = 45 0
B. ∠ (B ) = 45 0
C. ∠ (D ) = 45 0
D. ∠ (D ) = 60 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 6 2019
Chọn A. ∠ (C ) = 110 0
Ta có : ∠ (A )+ ∠ (D )= 180 0 ( hai góc trong cùng phía)
=> ∠ (D )= 180 0 - ∠ (A )= 180 0 - 70 0 = 110 0
mà ∠ (C )= ∠ (D ) (tính chất hình thang cân ) => ∠ (C )= ∠ (D )= 110 0
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
CM
21 tháng 1 2018
Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
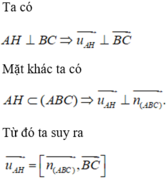
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.
Chọn C. (D ) = 45o
Ta có : hình thang ABCD CÓ BC//AD
=> ∠ (C )+ ∠ (D )= 180 0 ( hai góc trong cùng phía bù nhau)
mà ∠ C = 3 ∠ D nên 3 ∠ D+ ∠ D= 180 0 => ∠ D= 45 0