Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có:
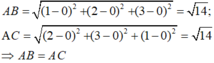
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.

Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)

Đáp án A
Vì đường thẳng d vuông góc với mặt phẳng (Oxy) nên đường thẳng d có vectơ chỉ phương là (0 ;0 ;1). Từ đó suy ra A là khẳng định sai.

A(1; 4), B(3; -2), C(4; 5)
Thay lần lượt tọa độ các đỉnh vào biểu thức P(x,y)= 2x – 5y + 3 ta có
P(1,4) = 2.1 – 5.4 + 3 = – 15, P(3, –2) = 2.3 – 5.( –2) + 3 = 19
P(4,5) = 2.4 – 5.5 + 3 = – 14
Do đó đường thẳng ∆ cắt các cạnh AB, BC và không cắt cạnh AC.
Đáp án C

a: Tọa độ I là:
\(\left\{{}\begin{matrix}x=\dfrac{-2+6}{2}=\dfrac{4}{2}=2\\y=\dfrac{4-2}{2}=1\end{matrix}\right.\)
b: A(1;3); I(2;1)
vecto AI=(1;-2)
PTTS của AI là;
x=1+t và y=3-2t
d: I(2;1); C(6;-2)
\(R=IC=\sqrt{\left(6-2\right)^2+\left(-2-1\right)^2}=5\)
Phương trình đường tròn đường kính BC là:
(x-2)^2+(y-1)^2=5^2=25
c: vecto BC=(8;-6)=(4;-3)
=>VTPT là (3;4)
Phương trình BC là:
3(x+2)+4(y-4)=0
=>3x+6+4y-16=0
=>3x+4y-10=0
Phương trình AH là:
4(x-1)+(-3)(y-3)=0
=>4x-4-3y+9=0
=>4x-3y+5=0
Tọa độ H là:
4x-3y+5=0 và 3x+4y-10=0
=>x=2/5 và y=11/5
H(0,4; 2,2); A(1;3)
\(AH=\sqrt{\left(1-0,4\right)^2+\left(3-2,2\right)^2}=1\)
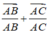

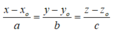

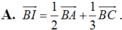
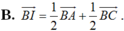
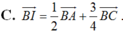
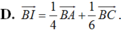
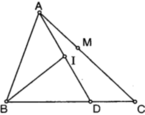

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.