Xét tính tăng, giảm của các dãy số u n , biết: u n = n - 1 n + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
9 tháng 2 2018
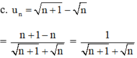
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
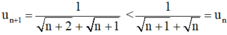
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
MM
1
AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
Với $n$ lẻ bất kỳ:
$u_n<0; u_{n+1>0; u_{n+2}< 0$
$\Rightarrow u_n< u_{n+1}> u_{n+2}$ với mọi $n$ lẻ bất kỳ
Do đó dãy không tăng cũng không giảm.
CM
20 tháng 5 2019
Ta có u n = n − 1 n + 1 = 1 − 2 n + 1
Xét hiệu u n + 1 − u n = 1 − 2 n + 2 − 1 − 2 n + 1
= 2 n + 1 − 2 n + 2 = 2 ( n + 2 ) − 2 ( n + 1 ) ( n + 1 ) . ( n + 2 ) = 2 ( n + 1 ) ( n + 2 ) > 0 ∀ n ∈ ℕ *
Kết luận dãy số ( u n ) là dãy số tăng.
Chọn đáp án D.
Với mọi n ∈ N có:
⇒ (un) là dãy số tăng.