Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 1 x trên 1 3 ; 3 . Tính 3 M + 2 m
A. 3 M + 2 m = 16 3
B. 3 M + 2 m = 15
C. 3 M + 2 m = 14
D. 3 M + 2 m = 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 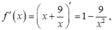
![]()
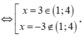
Có ![]()
![]()
Vậy m + M = 16.

Đáp án B.
ĐK: 0 ≤ x ≤ 1 . Với điều kiện này ta thấy rằng tử là nghịch biên (x tăng thì giá trị tử giảm đi) còn mẫu là đồng biến và mẫu dương (x tăng thì mẫu tăng theo) vì vậy tổng thể hàm y là hàm nghịch biến. Do đó M = max x ∈ 0 ; 1 y = y 0 = 1 ; m = min x ∈ 0 ; 1 y = y 1 = − 1 vậy M − m = 2.
Chọn C.
Phương pháp
- Tính y' và tìm nghiệm thuộc đoạn 1 3 ; 3 của y’.
- Tính giá trị của hàm số tại các điểm x = 1 3 ; x = 3 và các điểm vừa tìm được ở trên.
- So sánh các giá trị này và tìm GTLN, GTNN.
Cách giải: