

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

Chọn B
Nhìn vào đồ thị ta thấy: M = 6, m = -4
Vậy giá trị 2M + 3m = 2.6 + 3.(-4) = 0

Chọn A.
Xét hàm số y = x 4 2 - 4 x 2 + 1 trên [-1;3]
Ta có: ![]() Do đó
Do đó ![]()
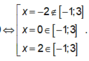
Lại có: ![]() và y(2) = -7
và y(2) = -7
Do đó ![]()
=> 2M + m = 11 - 7 = 4

Đáp án D
Ta có ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Ta có ![]()
 .
.
![]() .
.
Vậy m=2 và M = 11, do đó ![]() .
.

Chọn D.
Hàm số y = x 3 - 3 x 2 - 9 x + 1 xác định và liên tục trên R, nên trên đoạn [0;4] hàm số luôn xác định và liên tục.
Ta có: ![]()
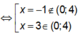
Khi đó: f(0) = 1; f(3) = -26; f(4) = -19
So sánh các giá trị trên ta được: ![]()
Suy ra: m + 2M = -26 + 2 = -24.
Vậy m + 2M = -24.

Chọn B
Xét g(x) = x 4 - 4 x 3 + 4 x 2 + a với x ∈ [0;2]
![]()
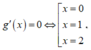
![]()
Bảng biến thiên g(x)
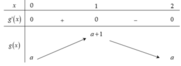
Trường hợp 1: a ≥ 0. Khi đó M = a + 1; m = a
Ta có M
≤
2m ![]() Với
Với 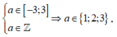
Trường hợp 2: ![]() Khi đó M = -a; m = -(a+1)
Khi đó M = -a; m = -(a+1)
Trường hợp 3: -1 < a < 0. Với 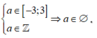
Vậy có 5 giá trị a cần tìm.