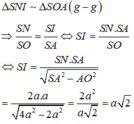Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Thể tích của khối cầu ngoại tiếp hình chóp đã cho bằng
![]()
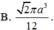
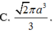
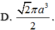
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

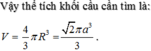

Chọn C.
Phương pháp:
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều.
Cách giải:


Đáp án D.
![]()
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên SO ⊥ (ABCD)
Từ giả thiết, ta có
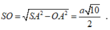
Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao
![]()
và bán kính đáy là
![]()
và bán kính đáy là
Suy ra
![]()
Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có SI.SO = SM.SB
![]()
Suy ra
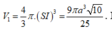
Do đó V 1 V 2 = 108 25
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhớ nhầm công thức tính thể tích khối cầu là
![]()
Do đó tính được V 1 V 2 = 324 25
Phương án B: Sai do HS nhớ nhầm công thức tính thể tích khối nón là
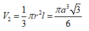
Do đó tính được V 1 V 2 = 18 30 25
Phương án C: Sai do HS nhớ sai công thức tính thể tích khối nón là
![]()
Do đó tính được V 1 V 2 = 36 25

Đáp án D

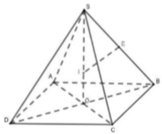
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên S O ⊥ ( A B C D )
Từ giả thiết, ta có S O = S A 2 - O A 2 = a 10 2 .
Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao h = S O = a 10 2 và bán kính đáy là r = O A = a 2 2 .
Suy ra V 2 = 1 3 πr 2 h = πa 3 10 12
Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có SI.IO = SM.SB ⇒ SI = S B 2 2 S O = 3 a 10 10
Suy ra V 1 = 4 3 π . ( SI ) 3 = 9 πa 3 10 25 . Do đó V 1 V 2 = 108 25

Đáp án: D
Hướng dẫn giải:
Gọi O là giao điểm của AC và BD, M là trung điểm của SA.
Qua M kẻ đường thẳng vuông góc với SA cắt SO tại I
⇒ I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
⇒ S I = R = 2
Ta có:
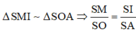
⇒ S O = S M . S A S I = S A 2 2 2
![]()
⇒ S A = S O 2
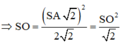
![]()
⇒ A B = 2 ⇒ S A B C D = A B 2 = 4
⇒ V S . A B C D = 1 3 . S O . S A B C D = 4 2 3

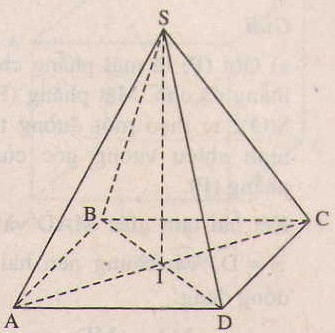
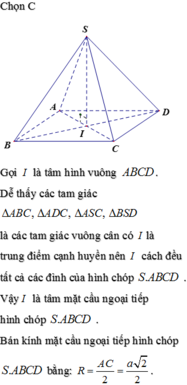
Gọi I = AC ∩ BD. Ta thấy AC = a√2 = BD,
SA = SC = a, nên SA2 + SC2 = AC2. Vậy điểm S nhìn AC dưới một góc vuông. Các điểm B và D cũng nhìn AC dưới một góc vuông.
Vậy mặt cầu ngoại tiếp hình chóp là mặt cầu đường kính AC. Tâm của cầu là điểm I và bán kính R = 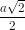 . Ta thấy rằng điểm I cũng là chân đường cao hạ từ đỉnh S xuống đáy.
. Ta thấy rằng điểm I cũng là chân đường cao hạ từ đỉnh S xuống đáy.

Chon B.
Phương pháp:
Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu. Từ đó tính bán kính mặt cầu.
Cách giải:
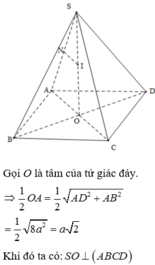
=>SO là trục của đường tròn ngoại tiếp tứ giác ABCD.
Trong mặt phẳng (SOA), vẽ đường trung trực của cạnh SA, cắt SO tại I.
=>I là tâm mặt cầu ngoại tiếp hình chóp.
Ta có: