Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng △ : x = 1 + t y = 1 + m t z = - 2 t và mặt cầu
(S): x 2 + y 2 + z 2 - 2x + 4y - 2z + 2 = 0 Với điều kiện nào của m thì đường thẳng Δ cắt (S) tại hai điểm phân biệt?
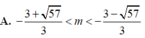
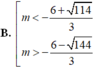
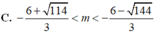
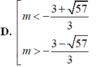
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án D.

Mặt khác lấy A(1;2;1) ∈ d thay vào phương trình mặt phẳng (P) thấy không thảo mãn (2)
Từ (1) và (2) có d ∥ P

Đáp án D
Phương pháp:
Đường thẳng d: x - x 0 a = y - y 0 b = z - z 0 c có 1 VTCP là a → = a ; b ; c
Cách giải: Đường thẳng d có 1 VTCP là a → = 3 ; - 2 ; 1

Đáp án B
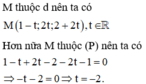
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án D
Phương pháp:
Đường thẳng
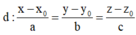
có 1 VTCP là u → = ( a ; b ; c )
Cách giải: Đường thẳng d có 1 VTCP là u → = ( 3 ; - 2 ; 1 )

Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Chọn B
Mặt cầu (S) có tâm I(1;−2;1), bán kính R=2.
là véctơ chỉ phương của đường thẳng Δ.
Để đường thẳng cắt mặt cầu (S) tại hai điểm phân biệt thì khoảng cách từ tâm I đến đường thẳng Δ phải nhỏ hơn bán kính R.