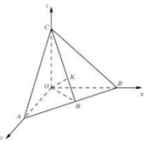
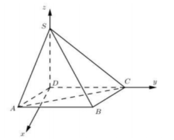
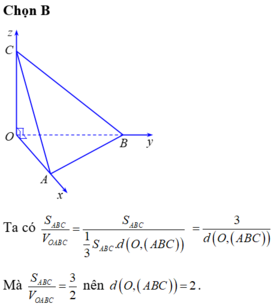
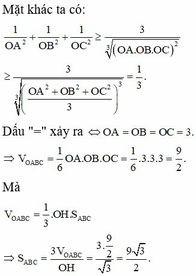
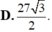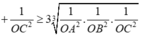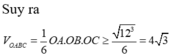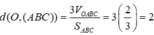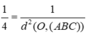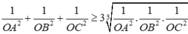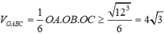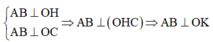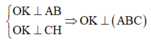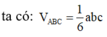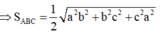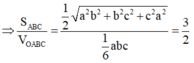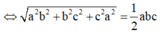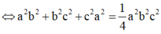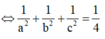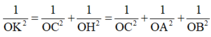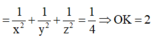Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng 3 2 Khối diện OABC có thể tích nhỏ nhất bằng
![]()
![]()