Cho khối lăng trụ ABC.A’B’C’. Gọi E là trọng tâm tam giác A’B’C’ và F là trung điểm BC. Tính tỉ số thể tích giữa khối B’.EAF và khối lăng trụ ABC.A’B’C’.
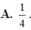
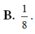
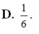
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Gọi M là trung điểm của B ' C ' ⇒ A , M , P thẳng hàng.
Do đó S P A Q = 1 2 S A A ' M Q .
V B ' . P A Q = 1 2 V B ' . A A ' M Q . Dễ thấy
V B ' . A B Q = 1 3 V B ' A ' M . B A Q ⇒ V B ' . A A ' M Q = 2 3 V B ' A ' M . B A Q = 2 3 . 1 2 V A ' B ' C ' . A B C
⇒ V P A Q = 1 2 . 2 3 . 1 2 .3 V A ' . A B C = 1 2 V A ' A B C .
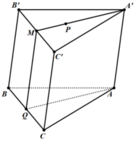

Phương pháp
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ V = S.h với S là diện tích đáy và h là chiều cao lăng trụ
Cách giải:
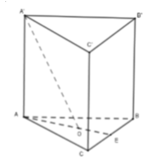
Gọi E là trung điểm của BC.

Chọn A

Đáp án A
Phương pháp : Hình chóp và lăng trụ có cùng chiều cao và diện tích đáy thì V C = 1 3 V L T .
Cách giải: Dễ thấy mặt phẳng (A’BC) chia khối lăng trụ thành 2 phần là khối đa diện A’B’C’BC và chóp A’.ABC.
⇒ V A B C . A ' B ' C ' = V A ' B ' C ' B C + V A ' A B C
Mà: V A ' A B C = 1 3 V A B C . A ' B ' C ' ⇒ V A ' B ' C ' B C + 2 3 V A B C . A ' B ' C '

Đáp án B
Phương pháp giải:
Dựng hình, xác định khoảng cách giữa hai đường thẳng chéo nhau để tính chiều cao lăng trụ
Lời giải: Gọi M là trung điểm của BC.
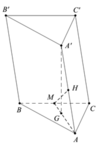
Ta có 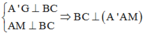
Kẻ ![]() => MH là đoạn vuông góc chung của BC, AA’
=> MH là đoạn vuông góc chung của BC, AA’
![]()
Mà ![]()
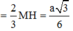
Xét tam giác vuông AA’G có : 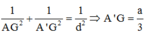
Vậy thể tích cần tính là: 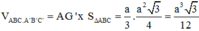
Chọn đáp án D