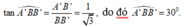Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB = BC = a, BB' = a 3 . Tính góc giữa đường thẳng A'B và mặt phẳng (BCC'B').
A. 60 °
B. 90 °
C. 45 °
D. 30 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN B
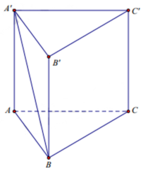
Ta có tan A ' B B ' ⏜ = A ' B ' B B ' = a a 3 = 1 3 ⇒ A ' B B ' ⏜ = 30 °

Gọi D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AD\perp BC\\AD=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
Gọi E là trung điểm BD \(\Rightarrow\) HE là đường trung bình tam giác ABD
\(\Rightarrow\left\{{}\begin{matrix}HE||AD\Rightarrow HE\perp BC\\HE=\dfrac{1}{2}AD=\dfrac{a\sqrt{3}}{4}\end{matrix}\right.\)
Mà \(B'H\perp\left(ABC\right)\Rightarrow B'H\perp BC\Rightarrow BC\perp\left(B'HE\right)\)
\(\Rightarrow\widehat{B'EH}\) là góc giữa (BCC'B') và đáy
\(\Rightarrow\widehat{B'HE}=60^0\)
\(\Rightarrow B'H=HE.tan60^0=\dfrac{3a}{4}\)
\(AA'||BB'\Rightarrow AA'||\left(BCC'B'\right)\Rightarrow d\left(AA';BC\right)=d\left(AA';\left(BCC'B'\right)\right)=d\left(A;\left(BCC'B'\right)\right)\)
Mà H là trung điểm AB \(\Rightarrow AB=2HB\Rightarrow d\left(A;\left(BCC'B'\right)\right)=2d\left(H;\left(BCC'B'\right)\right)\)
Từ H kẻ \(HK\perp B'E\)
Do \(BC\perp\left(B'HE\right)\Rightarrow\left(BCC'B'\right)\perp\left(B'HE\right)\)
Mà B'E là giao tuyến (B'HE) và (BCC'B')
\(\Rightarrow HK\perp\left(BCC'B'\right)\Rightarrow HK=d\left(H;\left(BCC'B'\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{B'H^2}+\dfrac{1}{HE^2}\Rightarrow HK=\dfrac{B'H.HE}{\sqrt{B'H^2+HE^2}}=\dfrac{3a}{8}\)
\(\Rightarrow d\left(AA';BC\right)=2HK=\dfrac{3a}{4}\)

Chọn D
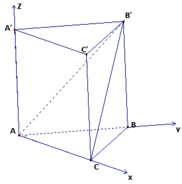
Vì tam giác ABC vuông cân tại A, cạnh BC = a√6 nên AB = AC = a√3.
Chọn hệ trục tọa độ Oxyz sao cho A (0;0;0), B (0; a√3; 0), C (a√3;0;0), A' (0;0;z) (z > 0).
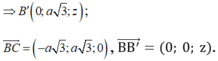
VTPT của (BCC'B') là:
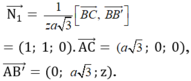
VTPT của mặt phẳng (BA'C) là:
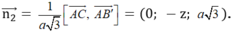
Vì góc giữa mặt phẳng và mặt phẳng bằng nên:
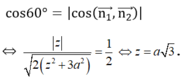
Vậy thể tích của khối lăng trụ ABC.A'B'C' là:
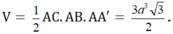
Chọn D.
Ta có: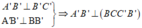 nên BB' là hình chiếu của A'B trên (BCC'B')
nên BB' là hình chiếu của A'B trên (BCC'B')
Vậy góc giữa đường thẳng A'B và mặt phẳng (BCC'B') là góc giữa hai đường thẳng A'B và BB' và là góc A ' B B ' ^
Lại có: