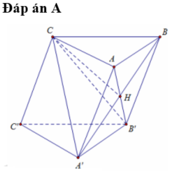
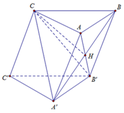
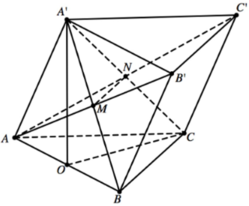
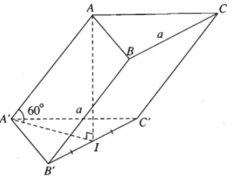
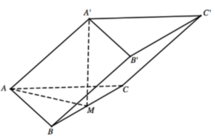
Cho hình lăng trụ A B C . A ' B ' C ' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng A B B ' A ' là tâm của hình bình hành A B B ' A ' . Thể tích khối lăng trụ A B C . A ' B ' C ' tính theo a là:
A. a 3 2 4
B. a 3 2 12
C. a 3 3
D. a 3 3 4

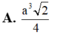
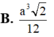
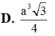



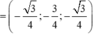
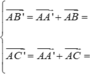
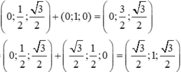
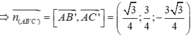
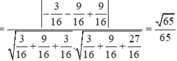
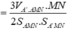
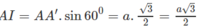
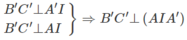


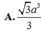


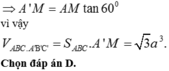
Đáp án A
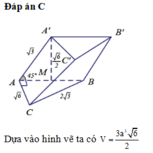
Gọi H là tâm của hình bình hành ABB'A'.
Khi đó C H ⊥ A B B ' A ' .
Do H là tâm của hình bình hành nên các tam giác C A ’ B ; C A B ’
là các tam giác cân tại C ( Do trung tuyến đồng thời là đường cao).
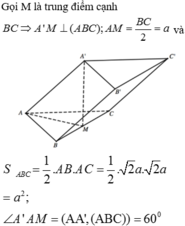
Khi đó C B = C A ' = a ; C A = C B ' = a . Suy ra C C ’ A ’ B ’ là tứ diện đều cạnh a. Tính nhanh ta có:
V C . C ' A ' B ' = a 3 2 12 ⇒ V A B C . A ' B ' C ' = a 3 2 4 .