Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

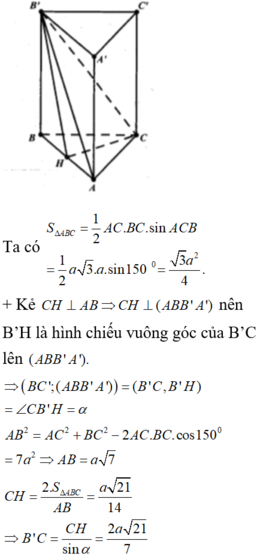
Đáp án A
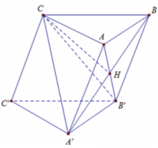
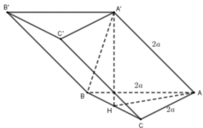
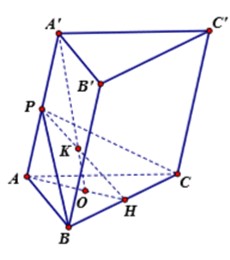
Gọi H là tâm của hình bình hành ABB'A'.
Khi đó C H ⊥ A B B ' A ' .
Do H là tâm của hình bình hành nên các tam giác C A ’ B ; C A B ’
là các tam giác cân tại C ( Do trung tuyến đồng thời là đường cao).
Khi đó C B = C A ' = a ; C A = C B ' = a . Suy ra C C ’ A ’ B ’ là tứ diện đều cạnh a. Tính nhanh ta có:
V C . C ' A ' B ' = a 3 2 12 ⇒ V A B C . A ' B ' C ' = a 3 2 4 .

Gọi O là trung điểm cạnh
A
B
⇒
A
'
O
⊥
A
B
C
và ![]()
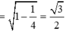
Vì vậy ![]()
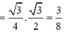
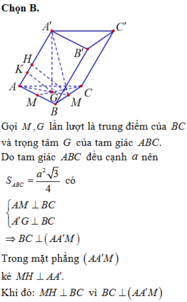
Chọn đáp án B.

Gọi M là trung điểm BC: BC = 2a; AG = 2 3 AI = 2 a 3 ; A ' A G ^ = 60 o .
Suy ra: A ' G = A G tan 60 o = 2 a 3 3
Ta có: V = S A B C . A ' G = 1 2 AB.AC.A'G
= 1 2 a. a 3 . 2 a 3 3 = a 3
Vậy V 3 + V a 3 - 1 = a
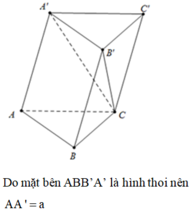
Đáp án B

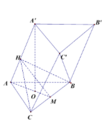
Gọi M là trung điểm BC. Từ M kẻ M H ⊥ A A ' ⇒ H B C ⊥ A A '
H M = 2 d t H B C B C = 2 a 2 3 8 a = a 3 4
A H = A M 2 - H M 2 = 3 a 2 4 - 3 a 2 16 = 3 a 4
∆ A M H ~ ∆ A A ' O ⇒ A H A O = M H A ' O ⇒ A ' O = A O . M H A H = a . a 3 . 4 3 . 4 . 3 a = a 3
Vậy thể tích ABCA’B’C' là
V = A O . d t A B C = a 3 . a 2 3 4 = a 3 3 12
Đáp án cần chọn là D





Đáp án A