Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
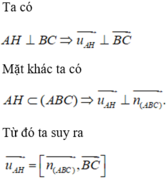
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.
A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)
\(a,\widehat{C}=180^0-\widehat{A}-\widehat{B}=75^0\\ b,=180^0-\widehat{C}=105^0\\ c,\text{Đề trùng câu b}\)
a) Xét tam giác ABC có:
\(\widehat{BAC}\) \(\text{+}\) \(\widehat{ABC}\) \(\text{+}\) \(\widehat{ACB}\) \(=180^o\) (Tổng 3 góc trong tam giác).
Thay số: \(60^o+45^o+\) \(\widehat{ACB}\) \(=180^o\).
\(\Rightarrow\) \(\widehat{ACB}\) \(=75^o.\)
b) Số đo góc ngoài đỉnh C là:
\(180^o-\) \(\widehat{ACB}\) = \(180^o-\) \(75^o=105^o.\)
a, Xét tam giác ADB và tam giác CDI có:
góc ADB = góc CDI (đối đỉnh)
góc BAD = góc DCI (gt)
Do đó: Tam giác ADB đồng dạng với tam giác CDI (g.g) (1)
Suy ra: góc ABD = góc DIC
b, Tam giác ADB đồng dạng với tam giác ACI (g.g) (2)
Suy ra: AD/AC = AB/AI
c, Từ (1),ta thấy: AD/CD = DB/DI nên AD.DI = BD.BC
Từ (2),ta có: AD/AC = AB/AI nên AD.AI = AB.AC
Do đó: AD(AI-DI) = AB.AC - BD.BC
AD^2 = AB.AC -BD.BC
Bài bạn đưa ra hơi khó đấy.Chúc bạn học tốt.
C
C