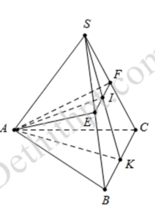
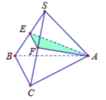
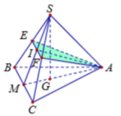
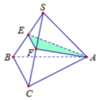
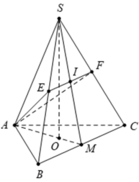
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Tính thể tích V của khối chóp S.ABC.
A. V = a 3 5 24
B. V = a 3 5 8
C. V = a 3 5 24
D. V = a 3 6 12

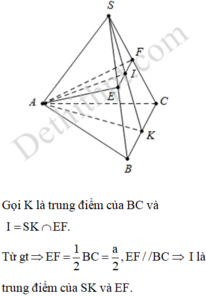

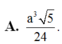
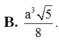
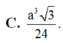
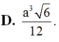

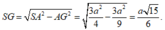


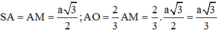
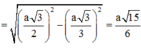
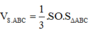
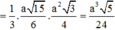
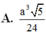
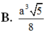
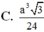
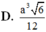
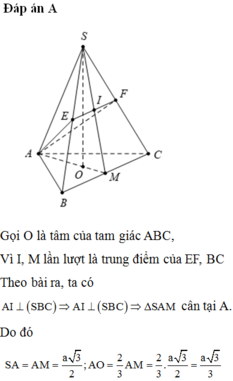
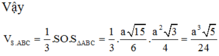

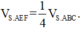
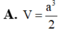
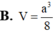
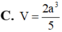
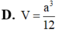
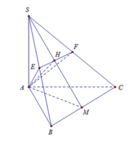

Đáp án A.
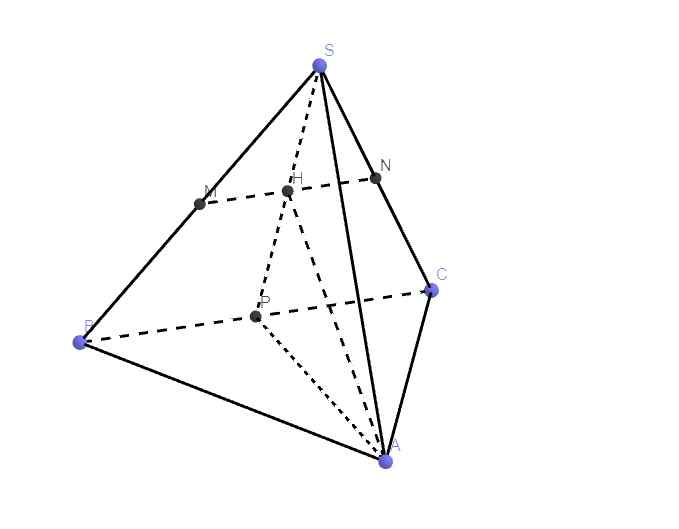
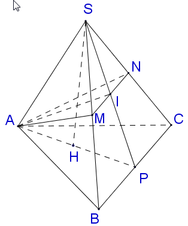
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, do S.ABC là hình chóp đều nên S O ⊥ A B C
Gọi M, N lần lượt là trung điểm của BC và EF.
Ta có S, M, N thẳng hàng và S M ⊥ B C tại M, S M ⊥ E F tại N.
Vì E, F lần lượt là trung điểm của SB, SC nên N là trung điểm của SM