Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
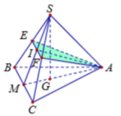
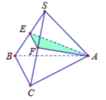
Gọi M là trung điểm BC, I = EF ∩ SM, suy ra I là trung điểm EF và SM.
Có ![]() => AF = AE => AEF cân tại A => AI
⊥
EF.
=> AF = AE => AEF cân tại A => AI
⊥
EF.
Tam giác ASM có AI ⊥ SM và I là trung điểm SM nên ASM cân tại A, suy ra SA = AM = a 3 2 .
Gọi G là trọng tâm tam giác ABC ![]()
Trong tam giác SAG có: 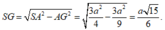
Vậy thể tích khối chóp S.ABC là ![]()

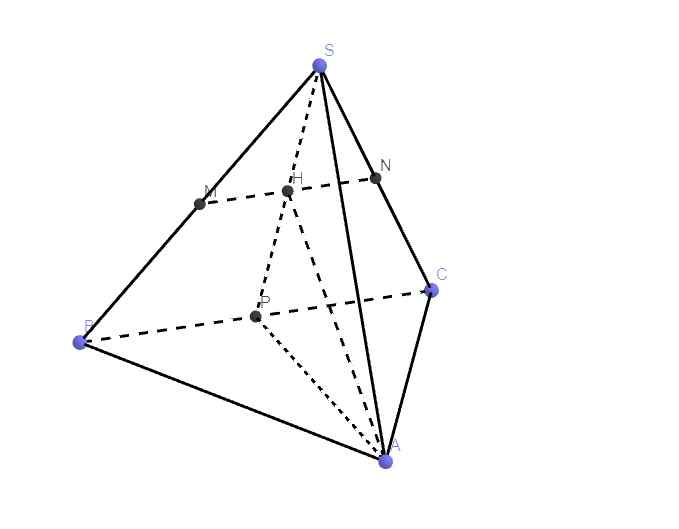
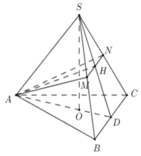
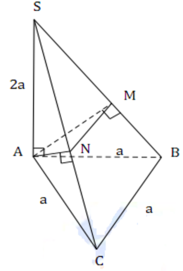
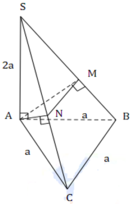
Gọi H là trung điểm MN \(\Rightarrow SH\perp MN\)
Do chóp SABC đều \(\Rightarrow\Delta AMN\) cân tại A \(\Rightarrow AH\perp MN\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH\perp SH\)
Nối SH kéo dài cắt BC tại P \(\Rightarrow\) P là trung điểm BC đồng thời H là trung điểm SP (Talet)
\(\Rightarrow\) AH là đường cao đồng thời là trung tuyến trong tam giác SAP
\(\Rightarrow\Delta SAP\) cân tại A
\(\Rightarrow SA=AP=\dfrac{a\sqrt{3}}{2}\)
\(SH=\dfrac{1}{2}\sqrt{SB^2-BP^2}=\dfrac{1}{2}\sqrt{SA^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{2}}{4}\)
\(MN=\dfrac{1}{2}BC=\dfrac{a}{2}\) ; \(HP=SH=\dfrac{a\sqrt{2}}{4}\)
\(AH=\sqrt{SA^2-SH^2}=\dfrac{a\sqrt{10}}{4}\)
\(V=\dfrac{1}{3}AH.\dfrac{1}{2}\left(MN+BC\right).HP=...\)

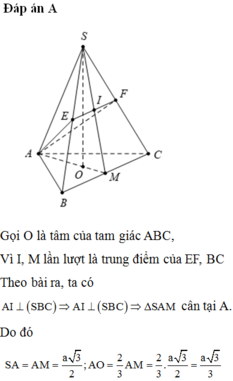
Đáp án A
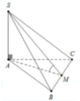
Gọi M là trung điểm của BC, ∆ S B C đều ⇒ S M ⊥ B C
Mà S A ⊥ ( A B C ) ⇒ S A ⊥ B C và S M ⊥ B C suy ra B C ⊥ ( S A M )
Ta có:
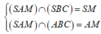
![]()
Xét tam giác SAM vuông tại A có:
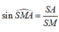
![]()
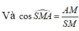
![]()
⇒ S A B C = 1 2 A M . B C = 3 a 2 8
⇒ V S . A B C = 1 3 S A . S A B C = a 3 3 32
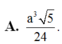
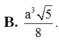
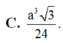
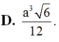
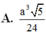
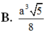
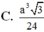
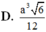
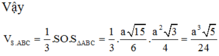
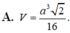
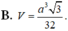
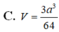
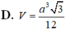

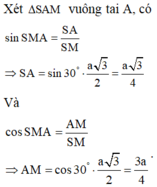
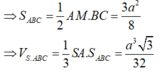
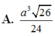
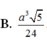
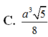
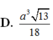



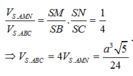
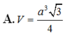
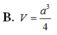
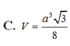
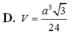

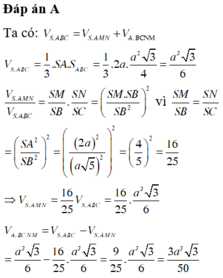
Đáp án A.