Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính diện tích S của mặt cầu ngoại tiếp hình chóp đã cho.
A. S = 16 πa 2 9
B. S = 64 πa 2 9
C. S = 16 πa 2 3
D. S = 64 πa 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

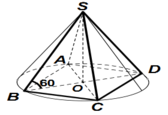
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
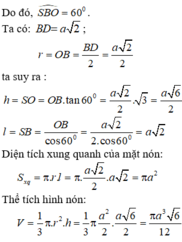

Đáp án C
Gọi M là trung điểm BC.
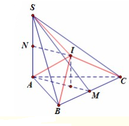
Dễ dàng chứng minh ∠ S B C , A B C = ∠ S M A = 60 °
⇒ S A = A M 3 = 3 2 . Đây là khối chóp có cạnh bên
vuông góc đáy nên bán kính mặt cầu ngoại tiếp được tính là: R 2 = S A 2 2 + 2 A M 3 2 = 43 48 ⇒ S = 4 πR 2 = 43 π 12 .

Đáp án A
Gọi O là tâm của tam giác A B C ⇒ S A ; A B C ^ = S A ; O A ^ = S A O ^ = 60 °
tam giác SAO vuông tại O, có
tan S A O ^ = S O O A ⇒ S O = tan 60 ° . a 3 3 = a ⇒ S A = O A 2 + S O 2 = 2 a 3 3
bán kính mặt cầu ngoại tiếp khối chóp là R = S A 2 2. S O = 2 a 3
vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 a 3 3 = 32 π a 3 81
Chọn đáp án A