Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM//SA
![]()
=> OM là trục của đường tròn ngoại tiếp tam giác ABC,
=> OA = OB = OC
Mặt khác, tam giác SAC vuông tại A, do đó OA = OS = OC
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABC có thể tích 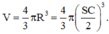
A là hình chiếu của S lên mặt phẳng (ABC), do đó góc ![]()
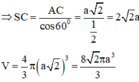

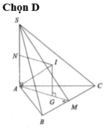
Gọi G là trọng tâm của tam giác đều ABC, suy ra G là tâm đường tròn ngoại tiếp DABC
Trục của đường tròn ngoại tiếp DABC cắt mặt phẳng trung trực của cạnh bên SA tại tâm I của mặt cầu ngoại tiếp hình chóp S.ABC. Tính
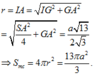

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà


Chọn D.
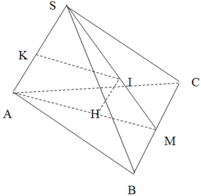
H là tâm của tam giác ABC, M là trung điểm của BC
Trong mp(SAM) dựng đt ss với SA cắt trung trực của SA tại I suy ra I là tâm mặt cầu ngoại tiếp
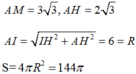

Đáp án D
Gọi H là trung điểm của BC ta có: A H ⊥ B C Do A B C ⊥ S B C ⇒ A H ⊥ S B C
Đặt A H = x ⇒ H C = a 2 − x 2 = H B = S H ⇒ Δ S B C
vuông tại S (do đường trùng tuyến bằng cạnh đối diện). Suy ra B C = S B 2 + S C 2 = a 3 . Gọi O là tâm đường tròn ngoại tiếp Δ A B C ⇒ O ∈ A H ⇒ O A = O B = O C = OS .Ta có: R = R A B C = A C 2 sin B , trong đó sin B = A H A B = A S 2 − S H 2 A B = 1 2 Do đó R C = a ⇒ S x q = 4 π R 2 C = 4 π a 2 .
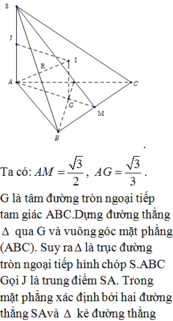



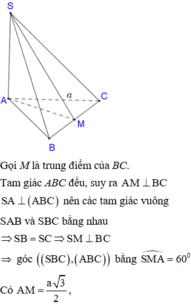
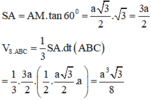

Đáp án C
Gọi M là trung điểm BC.
Dễ dàng chứng minh ∠ S B C , A B C = ∠ S M A = 60 °
⇒ S A = A M 3 = 3 2 . Đây là khối chóp có cạnh bên
vuông góc đáy nên bán kính mặt cầu ngoại tiếp được tính là: R 2 = S A 2 2 + 2 A M 3 2 = 43 48 ⇒ S = 4 πR 2 = 43 π 12 .