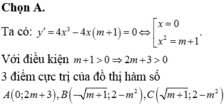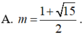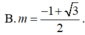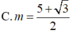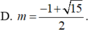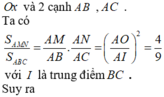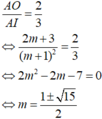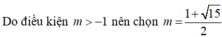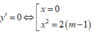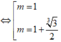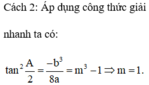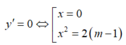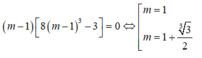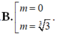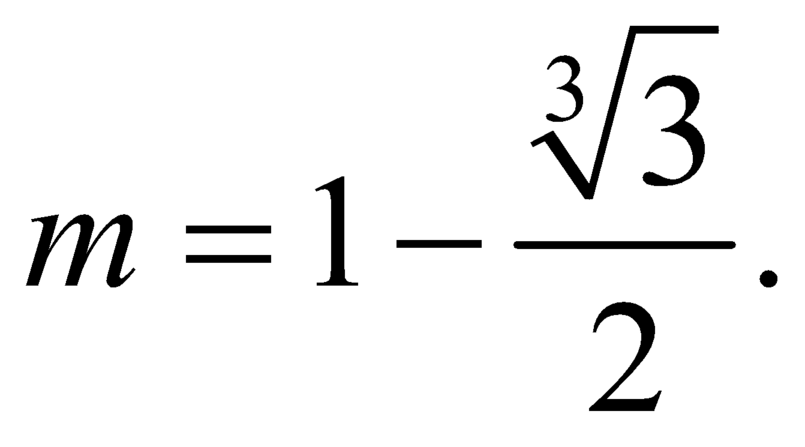Tìm giá trị của tham số m để đồ thị hàm số y=x4-2(m+1)x2+2m+3 có 3 điểm cực trị A,B,C là ba đỉnh của một tam giác, trục hoành chia tam gíac ABC thành một tam giác và một hình thang sao cho tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4/9
![]()
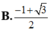
![]()
![]()