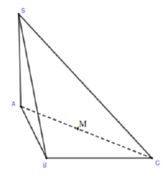
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a, BAC= 60 o . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
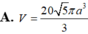
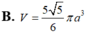
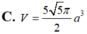
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án B
Phương pháp:
- Chứng minh Δ A B C vuông tại B, tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.
- Sử dụng công thức R 2 = h 2 4 + r 2 với R là bán kính hình cầu ngoại tiếp khối chóp, h là chiều cao, r là bán kính đường tròn ngoại tiếp đa giác đáy.
Cách giải:
Ta có: cos 60 ° = 1 2 = a 2 a → cos B A C = A B A C
⇒ Δ A B C vuông tại B.
Gọi M là trung điểm AC.
⇒ M là tâm đường tròn ngoại tiếp Δ A B C
⇒ M A = M A = A C 2 = a

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.
R là bán kính mặt cầu ngoại tiếp hình chóp.
h là chiều cao hình chóp.
Ta có công thức sau:
R 2 = h 2 4 + r 2 ⇒ R 2 = a 2 4 + a 2 = a 5 2
⇒ V = 4 3 π R 3 = 5 a 5 6
Chú ý khi giải:
HS cần linh hoạt trong việc chứng minh Δ A B C vuông tại B và biết sử dụng công thức liên hệ giữa R, r, h.

Lời giải:
Gọi $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$, $K$ là tâm đường tròn ngoại tiếp $ABC$ thì $IK\parallel SA$.
Ta có:
\(IS=IA\Leftrightarrow (\overrightarrow{IS})^2=IA^2\)
\(\Leftrightarrow (\overrightarrow{IA}+\overrightarrow{AS})^2=IA^2\)
\(\Leftrightarrow AS^2+2\overrightarrow{IA}.\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2(\overrightarrow{IK}+\overrightarrow{KA})\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2\overrightarrow{IK}.\overrightarrow{AS}=0\)
Vì $\overrightarrow{IK}\parallel \overrightarrow{AS}$ nên tồn tại $k\in\mathbb{R}$ sao cho $\overrightarrow{IK}=k\overrightarrow{AS}$
Khi đó: $AS^2+2kAS^2=0$
$\Rightarrow k=-\frac{1}{2}$
$\Rightarrow \overrightarrow{IK}=\frac{-1}{2}\overrightarrow{AS}$
$\Rightarrow IK=\frac{1}{2}.AS=a$
Lại có:
$\frac{AC}{\sin B}=2AK\Rightarrow AK=a$
Áp dụng định lý pitago: $R=IA=\sqrt{IK^2+AK^2}=\sqrt{2}a$
Thể tích khối cầu:
$V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi a^3$

Đáp án C

Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM//SA
![]()
=> OM là trục của đường tròn ngoại tiếp tam giác ABC,
=> OA = OB = OC
Mặt khác, tam giác SAC vuông tại A, do đó OA = OS = OC
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABC có thể tích 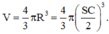
A là hình chiếu của S lên mặt phẳng (ABC), do đó góc ![]()