K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
26 tháng 3 2017
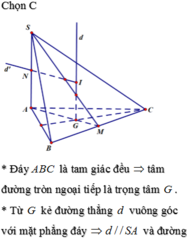
Đáp án B.
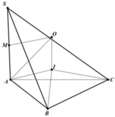
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
Ta có:
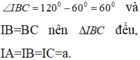
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
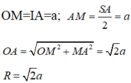
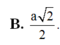
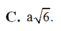
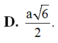


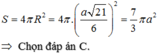
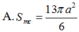

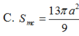
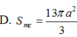

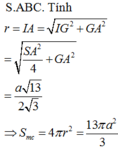
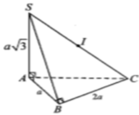

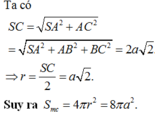
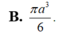
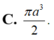
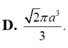



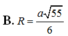
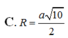
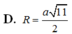

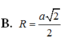
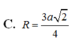
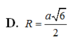

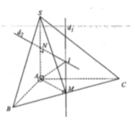
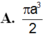
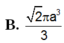

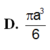
Lời giải:
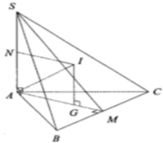
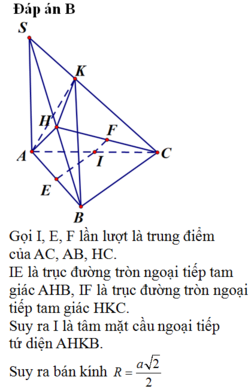
Gọi $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$, $K$ là tâm đường tròn ngoại tiếp $ABC$ thì $IK\parallel SA$.
Ta có:
\(IS=IA\Leftrightarrow (\overrightarrow{IS})^2=IA^2\)
\(\Leftrightarrow (\overrightarrow{IA}+\overrightarrow{AS})^2=IA^2\)
\(\Leftrightarrow AS^2+2\overrightarrow{IA}.\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2(\overrightarrow{IK}+\overrightarrow{KA})\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2\overrightarrow{IK}.\overrightarrow{AS}=0\)
Vì $\overrightarrow{IK}\parallel \overrightarrow{AS}$ nên tồn tại $k\in\mathbb{R}$ sao cho $\overrightarrow{IK}=k\overrightarrow{AS}$
Khi đó: $AS^2+2kAS^2=0$
$\Rightarrow k=-\frac{1}{2}$
$\Rightarrow \overrightarrow{IK}=\frac{-1}{2}\overrightarrow{AS}$
$\Rightarrow IK=\frac{1}{2}.AS=a$
Lại có:
$\frac{AC}{\sin B}=2AK\Rightarrow AK=a$
Áp dụng định lý pitago: $R=IA=\sqrt{IK^2+AK^2}=\sqrt{2}a$
Thể tích khối cầu:
$V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi a^3$