Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ và có một nguyên hàm là hàm số y = 1 2 x 2 - x + 1 . Giá trị của biểu thức ∫ 1 2 f ( x 2 ) d x bằng
A. - 4 3
B. 4 3
C. - 2 3
D. 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.

B
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau:
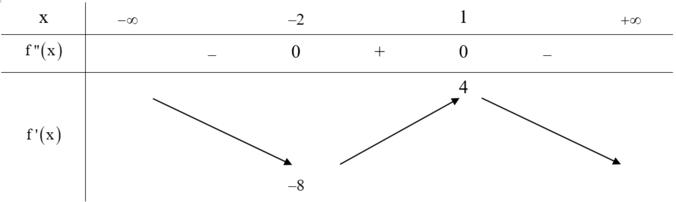

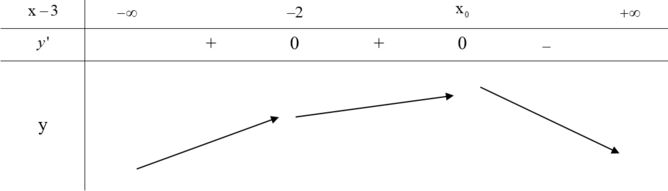
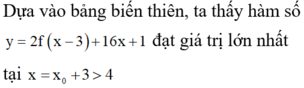

Chọn C.
Ta có f'(x)= 0
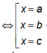
(Trong đó -2 < a < 0 < b < c < 2)
![]()
Ta có bảng xét dấuDựa vào bảng xét dấu ta thấy hàm số y = f(x) có 3 cực trị.
Đáp án B
Vì hàm số y = 1 2 x 2 - x + 1 là một nguyên hàm của hàm số y=f(x) nên