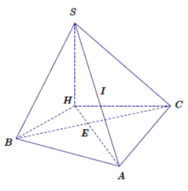
Hình chóp S . A B C có đáy ABC là tam giác vuông tại A , A B = a , A C = 2 a . Mặt bên S A B , S C A lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S . A B C là
A. R = a 2
B. R = a
C. R = 3 a 2
D. R = 3 a 2

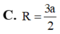
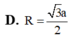

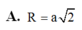
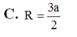
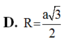


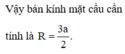

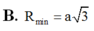
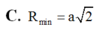



Đáp án C
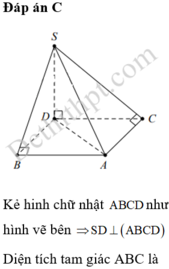
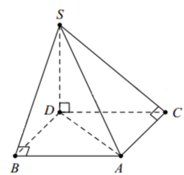
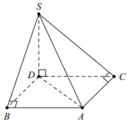
Kẻ hinh chữ nhật A B C D như hình vẽ bên ⇒ S D ⊥ A B C D
Diện tích tam giác ABC là S A B C = 1 2 . A B . A C = a 2
Suy ra V S . A B C = 1 3 . S D . S Δ A B C = a 2 3 . S D = 2 3 a 3 ⇒ S D = 2 a .
Bán kính mặt cầu ngoại tiếp khối chóp S . A B D C là
R = R A B D C 2 + S D 2 4 = a 5 2 2 + 2 a 2 4 = 3 a 2
Vậy bán kính mặt cầu cần tính là R = 3 a 2 .