Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có:
![]()
Gọi I là trung điểm của SC. Theo định lí ba đường vuông góc ta có tam giác SAC vuông tại A, mà tam giác SBC vuông tại B nên I cách đều các đỉnh của hình chóp hay I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta có bán kính: r = SC/2 = a

Đáp án B.
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
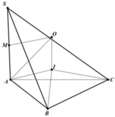
Ta có:
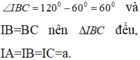
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
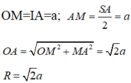

Đáp án C
Mặt cầu S(I,r) tiếp xúc với AB, SC lần lượt tại T, K. Khi đó ta có:
2r = IT + IK ≥ d(AB; SC) => r ≥ d(AB, SC)/2
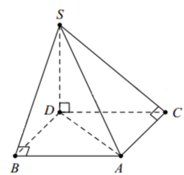
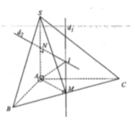
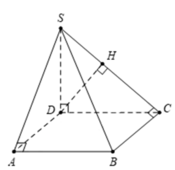
Dựng hình bình hành ABDC, khi đó ta có ABDC là hình vuông cạnh a. Hạ BH vuông góc với SD tại H. Khi đó ta có BH ⊥ (SCD).
Suy ra: d(SC; AB) = d(AB, (SCD)) = d(B; (SCD))
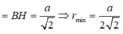

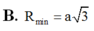
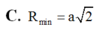

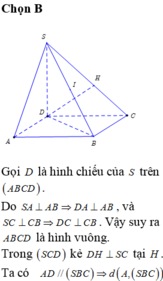

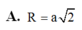
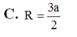
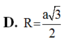

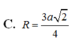
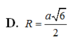

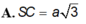
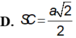





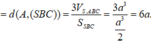

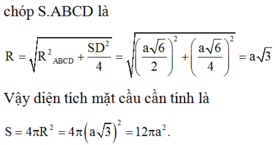
Đáp án A