Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, đường cao S H = a 3 3 . Tính góc giữa cạnh bên và mặt đáy của hình chóp
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
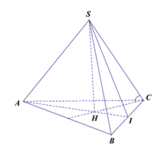
Gọi H là trọng tâm tam giác ABC, khi đó
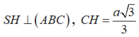
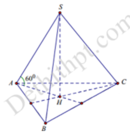
Góc giữa cạnh bên và mặt đáy là góc
![]()


\(+\) vì \(SH\perp\left(ABC\right)\) và \(AN\subset\left(ABC\right)\Rightarrow SH\perp AN\) hay \(\Rightarrow SH\perp AH\)
\(\Rightarrow\) \(AH\) là hình chiếu vuông góc của \(SA\) lên \(\left(ABC\right)\) \(\Rightarrow\left(SA,\left(ABC\right)\right)=\left(SA,AH\right)=\widehat{SAH}\)
\(+\) gọi \(M,N\) lần lượt là t/điểm \(AC,BC\)
vì \(\Delta ABC\) là tam giác đều cạnh \(a\) nên dễ tính được : \(AN=\dfrac{a\sqrt{3}}{2}\)
từ giả thiết , suy ra \(H\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow\) \(AH=\dfrac{2}{3}AN=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(+\) áp dụng hệ thức lược trong tam giác \(SHA\) vuông tại \(H\) , có :
\(tan\widehat{SAH}\) \(=\dfrac{SH}{AH}=\dfrac{a}{\dfrac{a\sqrt{3}}{3}}=\sqrt{3}\Rightarrow\widehat{SAH}\) \(=60^o\)

Đáp án A
Ta có: A H = 2 3 a 2 − a 2 2 = a 3 3
S A = A H cos 60 0 = a 3 3 1 2 = 2 a 3

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)
\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)

a. \(OC=\dfrac{2}{3}.2a.\dfrac{\sqrt{3}}{2}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{SCO}=\dfrac{SO}{OC}=\dfrac{3\sqrt{3}}{2}\) \(\Rightarrow\widehat{SCO}\simeq69^0\)
b. Gọi M là trung điểm BC \(\Rightarrow BC\perp\left(SAM\right)\)
Trong mp (SAM), từ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow\widehat{ASM}\) là góc giữa SA và (SBC)
\(SA=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{93}}{3}\)
\(SM=\sqrt{SA^2-\left(\dfrac{BC}{2}\right)^2}=\dfrac{2a\sqrt{21}}{3}\)
\(AM=a\sqrt{3}\)
Áp dụng định lý hàm cos:
\(cos\widehat{ASM}=\dfrac{SA^2+SM^2-AM^2}{2SA.MM}=...\)