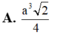
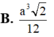
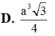
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
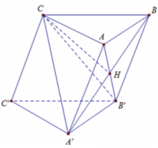
Gọi H là tâm của hình bình hành ABB'A'.
Khi đó C H ⊥ A B B ' A ' .
Do H là tâm của hình bình hành nên các tam giác C A ’ B ; C A B ’
là các tam giác cân tại C ( Do trung tuyến đồng thời là đường cao).
Khi đó C B = C A ' = a ; C A = C B ' = a . Suy ra C C ’ A ’ B ’ là tứ diện đều cạnh a. Tính nhanh ta có:
V C . C ' A ' B ' = a 3 2 12 ⇒ V A B C . A ' B ' C ' = a 3 2 4 .
Phương pháp
- Tính chiều cao A 'H .
- Tính thể tích khối lăng trụ V = S A B C . A ' H
Cách giải:
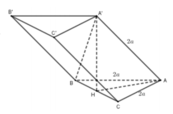
Tam giác ABC vuông cân đỉnh A cạnh AB = AC = 2a nên BC 
Tam giác AHA' vuông tại H nên
Vậy thể tích khối lăng trụ
Chọn B.
Đáp án A.
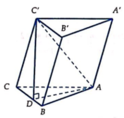
Theo giả thiết ta có CD' ⊥ (ABC). Áp dụng định lý Cô-sin cho ∆ ABD ta được:
AD = 
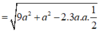
Hình chiếu vuông góc của AC’ trên mặt phẳng (ABC) là AD, vì vậy ta có góc giữa AC' và mặt phẳng (ABC) là góc C ' A D ^ = 45 0 => ∆ C'AD vuông cân tại D
Diện tích
∆
ABC là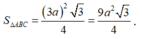 
Do đó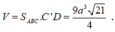 
Chọn B.
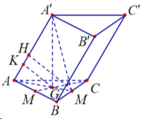
Gọi M,G lần lượt là trung điểm của BC và trọng tâm G của tam giác ABC.
Do tam giác ABC đều cạnh a nên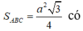 
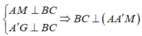
Trong mặt phẳng (AA'M) kẻ MH
⊥
AA'. Khi đó: 
Vậy MH là đoạn vuông góc chung của AA' và BC nên MH = a 3 4 .
Trong tam giác AA'G kẻ 
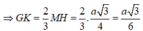
Xét tam giác AA'G vuông tại G ta có: 
Vậy thể tích của khối lăng trụ đã cho là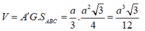 
Gọi O là trung điểm cạnh
A
B
⇒
A
'
O
⊥
A
B
C
và 
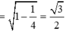
Vì vậy 
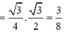
Chọn đáp án B.
