Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức z 4 + 3 i và số phức liên hợp của nó có điểm biểu diễn là N, N’. Biết rằng M, M’, N , N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z + 4 i − 5 .
A. 5 34 .
B. 2 5 .
C. 1 2 .
D. 4 13 .

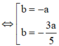
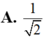
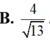
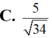
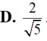



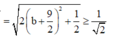

 ta có
ta có 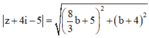
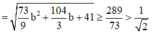


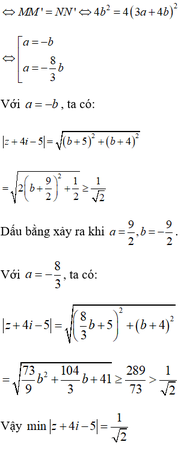

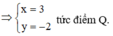
Đáp án C.
Giả sử z = a + b i
với a , b ∈ ℝ ⇒ M a , b , M ' a , − b .
Ta có:
z 4 + 3 i = a + b i 4 + 3 i = 4 a − 3 b + i 4 b + 3 a ⇒ N 4 a − 3 b ; 4 b + 3 a , N ' 4 a − 3 b ; − 4 b − 3 a
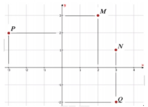
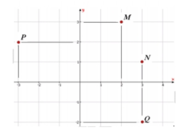
Để M, M’, N, N’ là 4 đỉnh của hình chữ nhật thì M phải có cùng tọa độ với N và N’
⇔ b = ± 4 b + 3 a ⇔ b = − a b = − 3 a 5 ⇒ M nằm trên đường thẳng Δ 1 : x + y = 0 hoặc Δ 2 : 3 x + 5 y = 0
Xét điểm I 5 ; − 4 ⇒ z + 5 i − 5 = M I = M i n d I , Δ 1 , d I , Δ 1 = 1 2 .