Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có
sin 5 x ≤ sin 4 x ⇒ y ≤ sin 4 x + 3 cos x
Áp dụng bất đẳng thức Cauchy ta có:
1 - cos x 1 + cos x 1 + cos x = 1 2 2 - 2 cos x 1 + cos x 1 + cos x
≤ 1 2 2 - 2 cos x + ( 1 + cos x ) 2 3 3 = 32 27 < 3
⇒ 3 - 1 - cos x 1 + cos x 2 > 0 ⇒ 1 - cos x 3 - 1 - cos x 1 + cos x 2 ≥ 0 ⇒ 3 1 - cos x - sin 4 x ≥ 0 ⇔ sin 4 x + 3 cos x ≤ 3
M = maxy = 3 ⇔ cos(x) = 1
⇔ x = k 2 π , k ∈ ℤ
Ta lại có
y ≥ - sin 4 x + 3 cos x
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có:
1 + cos x 1 - cos x 1 - cos x = 1 2 2 + 2 cos x 1 - cos x 2 ≥ 32 27 ≤ 3 ⇒ 3 - 1 + cos x 1 - cos x 2 > 0 ⇒ 1 + cos x 3 - 1 + cos x 1 - cos x 2 ⇔ sin 4 x + 3 cos x ≥ - 3 m = m i n y = - 3 ⇔ cos x = - 1 ⇔ x = k 2 π , k ∈ ℤ
Do đó M m = - 1 . Vì vậy, mệnh đề D sai.
Đáp án cần chọn là D
Ta có
y = sin x = cos 2 x = sin x - 1 - 2 sin 2 x = 2 sin 2 x + sin x - 1
Đặt t = sin(x), - 1 ≤ t ≤ 1
Ta sẽ đi tìm GTLN và GTNN của hàm số y = g t = 2 t 2 + t - 1 trên đoạn [ -1;1 ]
Ta có g t = - 2 t 3 - t + 1 , - 1 ≤ t ≤ 1 2 2 t 3 + t - 1 , 1 2 ≤ t ≤ 1
* Xét hàm số h t = - 2 t 3 - t + 1 trên đoạn - 1 ; 1 2
Dễ dàng tìm được
M a x r ∈ 1 2 ; 1 h t = 9 8 ⇔ t = - 1 4 M i n r ∈ 1 2 ; 1 h t = 0 ⇔ t = 1 2
* Xét hàm số k t = 2 t 3 + t - 1 trên đoạn 1 2 ; 1
Cũng dễ dàng tìm được
M a x r ∈ 1 2 ; 1 k t = 2 ⇔ t = 1 M i n r ∈ 1 2 ; 1 k t = 0 ⇔ t = 1 2
Qua hai trường hợp trên ta đi đến kết luận
M a x r ∈ - 1 ; 3 g t = 2 ⇔ t = 1 M i n r ∈ - 1 ; 3 g t = 0 ⇔ t = 1 2
Hay
M = M a x y = 2 ⇔ sin x = - 1 ⇔ x = - π 2 + k 2 π m = Miny = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án C
Đáp án B
Bảng biến thiên của hàm số trên 0 ; 9 2 có dạng như hình vẽ dưới đây.
Do đó GTLN của hàm số là f(0);f(2) hoặc f 9 2 ; GTNN của hàm số là f(1) hoặc f(4)
Mặt khác f 1 = f 2 - ∫ 1 2 f ' x d x ; f 4 = f 2 - ∫ 2 4 f ' x d x
Dựa vào hình vẽ ta có: ∫ 2 4 f ' x d x > ∫ 1 2 f ' x d x ⇒ f 4 < f 1 (loại C và D)
Mặt khác f 9 2 = f 4 + ∫ 4 9 2 f ' x d x ; f 0 = f 1 + ∫ 0 1 f ' x d x
Dựa vào hình vẽ ta có: ∫ 0 1 f ' x d x > ∫ 4 9 2 f ' x d x f 1 > f 4 ⇒ f 0 > f 9 2 .
Chọn D.
Xét hàm số 
hàm số liên tục trên R
Có 
đồng biến trên [2;4]
Nên 
Do đó 
Ta có 
Dấu bằng xảy ra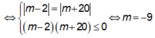 
Vậy 
Chọn D
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có
Do đó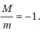
. Vì vậy, mệnh đề D sai.