Tìm nghiệm của phương trình 5 2018 x = 5 2018 .
A. x = 1 2
B. x = 1 − log 5 2
C. x = 2
D. x = − log 5 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2021
a) Ta có: \(A=x^6+5+xy-x-2x^2-x^5-xy-2\)
\(=x^6-x^5-2x^2-x+3\)
Bậc là 6
13 tháng 4 2021
b) Thay x=-1 và y=2018 vào A, ta được:
\(A=\left(-1\right)^6-\left(-1\right)^5-2\cdot\left(-1\right)^2-\left(-1\right)+3\)
\(=1-\left(-1\right)-2\cdot1+1+3\)
\(=1+1-2+1+3\)
=4
7 tháng 3 2022
b: \(\text{Δ}=\left(2m+3\right)^2-4\left(4m+2\right)\)
\(=4m^2+12m+9-16m-8\)
\(=4m^2-4m+1=\left(2m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm
Theo đề, ta có:
\(\left\{{}\begin{matrix}2x_1-5x_2=6\\x_1+x_2=2m+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1-5x_2=6\\2x_1+2x_2=4m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x_2=-4m\\2x_1=5x_2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\2x_1=\dfrac{20}{7}m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\x_1=\dfrac{10}{7}m+3\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=4m+2\)
\(\Rightarrow4m+2=\dfrac{40}{49}m^2+\dfrac{12}{7}m\)
\(\Leftrightarrow m^2\cdot\dfrac{40}{49}-\dfrac{16}{7}m-2=0\)
\(\Leftrightarrow40m^2-112m-98=0\)
\(\Leftrightarrow40m^2-140m+28m-98=0\)
=>\(20m\left(2m-7\right)+14\left(2m-7\right)=0\)
=>(2m-7)(20m+14)=0
=>m=7/2 hoặc m=-7/10
CM
7 tháng 6 2018
Đáp án A.
+ Điều kiện: x > 0
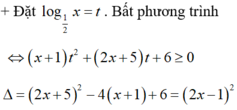
Bất phương trình
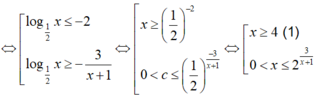
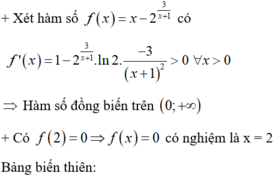
=> Bất phương trình x ≤ 2 3 x + 1 ⇔ f ( x ) ≤ 0 ⇔ 0 < x ≤ 2 ( 2 ) .
Từ (1) và (2) => Tập nghiệm của bất phương trình là
S = ( 0 ; 2 ] ∪ [ 4 ; + ∞ ) .
Vậy có 2016 nghiệm nguyên thỏa mãn.
CM
11 tháng 5 2017
Đáp án A.
+ Điều kiện: x > 0
+ Đặt log 1 2 x = t . Bất phương trình ⇔ x + 1 t 2 + 2 x + 5 t + 6 ≥ 0
Δ = 2 x + 5 2 − 4 x + 1 + 6 = 2 x − 1 2
Bất phương trình
⇔ log 1 2 x ≤ − 2 log 1 2 x ≥ − 3 x + 1 ⇔ x ≥ 1 2 − 2 0 < c ≤ 1 2 − 3 x + 1 ⇔ x ≥ 4 (1) 0 < x ≤ 2 3 x + 1
+ Xét hàm số f x = x − 2 3 x + 1 có f ' x = 1 − 2 3 x + 1 . ln 2. − 3 x + 1 2 > 0 ∀ x > 0
Hàm số đồng biến trên 0 ; + ∞
+ Có f 2 = 0 ⇒ f x = 0 coa nghiệm là x=2
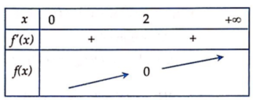
Bảng biến thiên:
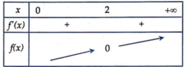
Bất phương trình x ≤ 2 3 x + 1 ⇔ f x ≤ 0 ⇔ 0 < x ≤ 2 ( 2 )
Từ (1) và (2) => Tập nghiệm của bất phương trình là S = 0 ; 2 ∪ 4 ; + ∞
Vậy có 2016 nghiệm nguyên thỏa mãn.
Đáp án A
Ta có:
5 2018 x = 5 2018 ⇔ 5 x 2018 = 5 2018 ⇔ 5 x = 5 ⇔ x = 1 2