Người ta dùng một thanh sắt tròn có độ dài ban đầu l 0 = 50 cm và tiết diện ngang S = 2,5 m m 2 . Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài ∆ l tương ứng của nó (Bảng 34-35. 1). Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.
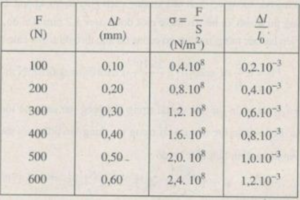

Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.
![]()
Từ đó tìm đươc suất đàn hồi :
![]()
và hệ số đàn hồi:
![]()


xét tam giác vuông \(ABC\)
ta có : \(AC=\sqrt{10^2-6^2}=\sqrt{64}=8\left(m\right)\)
vì thanh đồng chất tiếp diện đều nên ta có tâm \(G\) là trung điểm \(AB\)
xét tam giác vuông \(AGH\)
ta có : \(AH=AG.cos\widehat{GAH}=5.\dfrac{8}{10}=4\left(m\right)\)
áp dụng MÔ MEN ta có : \(\Sigma F\backslash\left(G\right)=\Sigma P\backslash\left(G\right)\)
\(\Leftrightarrow F.AC=P.AH\Leftrightarrow F.8=40.4\Leftrightarrow F=\dfrac{40.4}{8}=20\left(N\right)\)
vậy độ lớn của lực \(F\) là \(20\left(N\right)\)

Đáp án: D
Nhiệt độ để chiều dài của chúng bằng nhau:
l0nh(1 + anht) = l0s(1 + ast) (ban đầu t0 = 0 oC → ∆t = t)
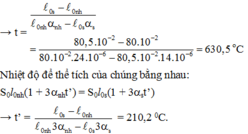
Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ
Chọn tỉ lệ vẽ trên các trục tọa độ:
- Trục hoành: 1 cm → σ = 0,5. 10 8 N/ m 2
- Trục tung: 1 cm → ε = 0,2. 10 - 3
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l0 của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:
ε = ∆ l/ l 0 = a ε
Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị: