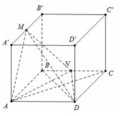
Cho hình lập phương ![]() có cạnh a. Gọi M là trung điểm A', B', N' là trung điểm Tính thể tích của khối tứ diện ADMN
có cạnh a. Gọi M là trung điểm A', B', N' là trung điểm Tính thể tích của khối tứ diện ADMN
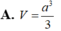
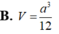
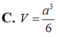
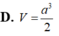
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

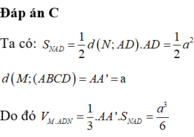

Đáp án C
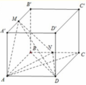
Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .

b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .

Chọn D
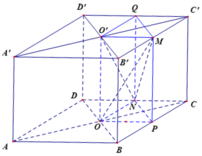
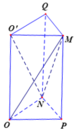
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24

Đáp án C
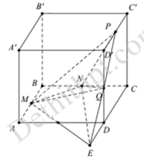
Dựng hình như hình vẽ
Ta có: V M N P Q = 1 2 V P . M N E = 1 2 . 1 3 .1. S M N E
Do M N / / A C ; M E / / B D ⇒ M N ⊥ M E ; M N = 2 2 ; M E = 2
Do đó S M N E = 1 2 ⇒ V M N P Q = 1 12
(ngoài ra các em có thể gắn các hệ trục tọa độ)